题目内容
9.已知x=$\sqrt{5}$+2,y=$\frac{1}{\sqrt{5}+2}$,求($\frac{{x}^{2}}{x-y}+\frac{{y}^{2}}{y-x}$)÷xy的值.分析 首先利用分式的混合运算法则化简分式,进而将已知化简代入求出即可.
解答 解:($\frac{{x}^{2}}{x-y}+\frac{{y}^{2}}{y-x}$)÷xy
=$\frac{{x}^{2}-{y}^{2}}{x-y}$×$\frac{1}{xy}$
=$\frac{x+y}{xy}$,
∵y=$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2,x=$\sqrt{5}$+2,
∴将x,y代入原式得:原式=2$\sqrt{5}$.
点评 此题主要考查了分式的混合运算以及二次根式的混合运算,正确化简分式以及二次根式是解题关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,在菱形ABCD中,对角线AC、BD相交于点O,E是AB的中点,如果EO=2,求四边形ABCD的周长.
如图,在菱形ABCD中,对角线AC、BD相交于点O,E是AB的中点,如果EO=2,求四边形ABCD的周长.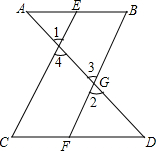 已知如图,∠1=∠2,∠B=∠C.求证:∠A=∠D.
已知如图,∠1=∠2,∠B=∠C.求证:∠A=∠D.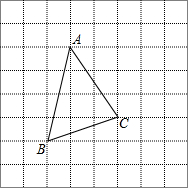 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.