题目内容
19．
如图，在菱形ABCD中，对角线AC、BD相交于点O，E是AB的中点，如果EO=2，求四边形ABCD的周长．
分析 根据菱形的性质可以判定O为BD的中点，结合E是AB的中点可知EO是△ABD的中位线，根据三角形中位线定理可知AD的长，于是可求出四边形ABCD的周长．
解答 解：∵四边形ABCD为菱形，
∴BO=DO，即O为BD的中点，
又∵E是AB的中点，
∴EO是△ABD的中位线，
∴AD=2EO=2×2=4，
∴菱形ABCD的周长=4AD=4×4=16．
点评 本题主要考查了菱形的性质，解答本题的关键是证明EO是△ABD的中位线，此题难度不大．
练习册系列答案
相关题目
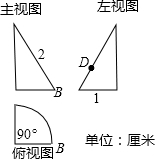如图是一个锥体的三视图．