题目内容
9.计算:(1)$\sqrt{6}×\sqrt{\frac{1}{2}}-\sqrt{12}$
(2)$\sqrt{(1-π)^{2}}-(\sqrt{π+1})^{2}+\frac{1}{\sqrt{2}-1}$.
分析 (1)先利用二次根式的乘法法则运算,然后把$\sqrt{12}$为最简二次根式后合并即可;
(2)先利用二次根式的性质化简,再分母有理化,然后合并即可.
解答 解:(1)原式=$\sqrt{6×\frac{1}{2}}$-2$\sqrt{3}$
=$\sqrt{3}$-2$\sqrt{3}$
=-$\sqrt{3}$;
(2)原式=π-1-(π+1)+$\sqrt{2}$+1
=π-1-π-1+$\sqrt{2}$-1
=$\sqrt{2}$-3.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列4个数中,3.1415926,$\frac{22}{7}$,π,$\sqrt{36}$,其中无理数是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{36}$ |
20.在$\frac{xy}{2}$、$\frac{1}{x}$、$\frac{a}{4}$、$\frac{5}{π}$、$\frac{3}{x+y}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.已知x-2y=3,则代数式6-2x+4y的值为( )
| A. | -3 | B. | -1 | C. | 0 | D. | 3 |
1.若x+$\frac{1}{x}$=2,则x2+$\frac{1}{x^2}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19. 如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积为8,若点A对应的数是-2,则B对应的数是( )
如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积为8,若点A对应的数是-2,则B对应的数是( )
 如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积为8,若点A对应的数是-2,则B对应的数是( )
如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积为8,若点A对应的数是-2,则B对应的数是( )| A. | 2$\sqrt{2}$-2 | B. | 2-2$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
 如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.
如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.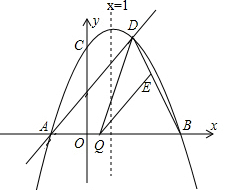 已知:如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
已知:如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m). 如图,将方格纸分成6个三角形,在②③④⑤⑥这5个三角形中,与三角形①相似的三角形有哪些?说明理由!
如图,将方格纸分成6个三角形,在②③④⑤⑥这5个三角形中,与三角形①相似的三角形有哪些?说明理由!