题目内容
15. 如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE=$\frac{3}{5}$.
如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE=$\frac{3}{5}$.
分析 连接EC,由90°的圆周角所对的弦为直径,根据∠EOC=90°得到EC为圆A的直径,所以点A在EC上且为EC中点,在直角三角形EOC中,由OE和OC的长,利用勾股定理求出EC的长,根据同弧所对的圆周角都相等得到∠EBO与∠ECO相等,而∠ECO在直角三角形EOC中,根据余弦函数定义即可求出sin∠ECO的值,进而得到sin∠EBO.
解答  解:连接EC,由∠EOC=90°得到BC为圆A的直径,
解:连接EC,由∠EOC=90°得到BC为圆A的直径,
∴EC过点A,
又OE=3,OC=4,根据勾股定理得:EC=5,
∵∠OBE和∠OCE为$\widehat{OE}$所对的圆周角,
∴∠OBE=∠OCE,
则sin∠OBE=sin∠OCE=$\frac{OE}{EC}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查学生掌握90°的圆周角所对的弦为直径以及同弧所对的圆周角相等,考查了数形结合以及转化的数学思想,是一道中档题.连接EC且得到EC为圆A的直径是解本题的突破点.

练习册系列答案
相关题目
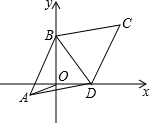 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.