题目内容
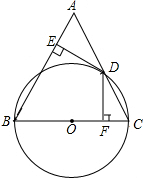 如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,
如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,①求证:ED是⊙O的切线;
②求证:DE2=BF•AE;
③若DF=3
| 5 |
| 2 |
| 3 |
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)根据圆周角定理由BC为⊙O的直径得到∠BDC=90°,再根据等腰三角形的性质得AD=CD,即D点为AC的中点,则可判断OD为△ABC的中位线,所以OD∥AB,而DE⊥AB,则DE⊥OD,然后根据切线的判定定理即可得到DE是⊙O的切线;
(2)根据等腰三角形的性质得BD平分∠ABC,则利用角平分线性质得DE=DF,再证明Rt△AED∽Rt△DFB,根据相似的性质得DE:BF=AE:DF,用DE代换DF根据比例的性质即可得到DE2=BF•AE;
(3)由于∠A=∠C,则cosA=cosC=
,在Rt△CDF中,利用余弦的定义得cosC=
=
,设CF=2x,则DC=3x,根据勾股定理计算得DF=
x,所以
x=3
,解得x=3,于是得到DC=9,在Rt△CBD中根据余弦的定义可计算出BC.
(2)根据等腰三角形的性质得BD平分∠ABC,则利用角平分线性质得DE=DF,再证明Rt△AED∽Rt△DFB,根据相似的性质得DE:BF=AE:DF,用DE代换DF根据比例的性质即可得到DE2=BF•AE;
(3)由于∠A=∠C,则cosA=cosC=
| 2 |
| 3 |
| CF |
| DC |
| 2 |
| 3 |
| 5 |
| 5 |
| 5 |
解答:(1)证明:∵BC为⊙O的直径,
∴∠BDC=90°,即BD⊥AC,
∵BA=BC,
∴AD=CD,即D点为AC的中点,
∵点O为BC的中点,
∴OD为△ABC的中位线,
∴OD∥AB,
而DE⊥AB,
∴DE⊥OD,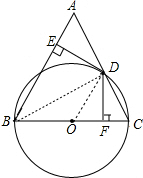
∴DE是⊙O的切线;
(2)证明:∵BA=BC,BD⊥AC,
∴BD平分∠ABC,
∴DE=DF,
∵∠ADE+∠BDE=90°,∠BDE+∠BDO=90°,
∴∠ADE=∠BDO,
而OB=OD,
∴∠BDO=∠OBD,
∴∠ADE=∠OBD,
∴Rt△AED∽Rt△DFB,
∴DE:BF=AE:DF,
∴DE:BF=AE:DE,
∴DE2=BF•AE;
(3)解:∵∠A=∠C,
∴cosA=cosC=
,
在Rt△CDF中,cosC=
=
,
设CF=2x,则DC=3x,
∴DF=
=
x,
而DF=3
,
∴
x=3
,解得x=3,
∴DC=9,
在Rt△CBD中,cosC=
=
,
∴BC=
×9=
,
即⊙O的直径为
.
∴∠BDC=90°,即BD⊥AC,
∵BA=BC,
∴AD=CD,即D点为AC的中点,
∵点O为BC的中点,
∴OD为△ABC的中位线,
∴OD∥AB,
而DE⊥AB,
∴DE⊥OD,

∴DE是⊙O的切线;
(2)证明:∵BA=BC,BD⊥AC,
∴BD平分∠ABC,
∴DE=DF,
∵∠ADE+∠BDE=90°,∠BDE+∠BDO=90°,
∴∠ADE=∠BDO,
而OB=OD,
∴∠BDO=∠OBD,
∴∠ADE=∠OBD,
∴Rt△AED∽Rt△DFB,
∴DE:BF=AE:DF,
∴DE:BF=AE:DE,
∴DE2=BF•AE;
(3)解:∵∠A=∠C,
∴cosA=cosC=
| 2 |
| 3 |
在Rt△CDF中,cosC=
| CF |
| DC |
| 2 |
| 3 |
设CF=2x,则DC=3x,
∴DF=
| DC2-CF2 |
| 5 |
而DF=3
| 5 |
∴
| 5 |
| 5 |
∴DC=9,
在Rt△CBD中,cosC=
| DC |
| BC |
| 2 |
| 3 |
∴BC=
| 3 |
| 2 |
| 27 |
| 2 |
即⊙O的直径为
| 27 |
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质、锐角三角函数的定义.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知-1≤a≤1,则x2+(a-4)x+4-2a>0的解为( )
| A、x>3或x<2 |
| B、x>2或x<1 |
| C、x>3或x<1 |
| D、1<x<3 |

 如图,已知?ABCD.
如图,已知?ABCD. 如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
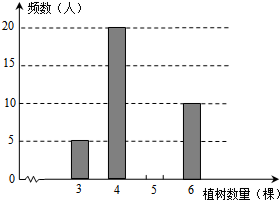 今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整). 如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为
如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为