题目内容
5.抛物线y=-x2+x+2与y轴的交点坐标是( )| A. | (1,2) | B. | (0,-1) | C. | (0,1) | D. | (0,2) |
分析 把x=0代入解析式求出y的值,根据y轴上点的特征和二次函数图象上点的坐标特征解答即可.
解答 解:当x=0时,y=2,
故抛物线y=-x2+x+2与y轴的交点坐标是(0,2).
故选:D.
点评 本题考查的是二次函数图象上点的坐标特征,掌握抛物线与y轴交点的纵坐标是函数解析中的c值是解题的关键.

练习册系列答案
相关题目
16.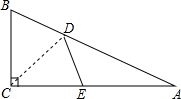 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )| A. | 46° | B. | 60° | C. | 68° | D. | 77° |
15. 如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
 如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )| A. | 313 | B. | 144 | C. | 169 | D. | 25 |
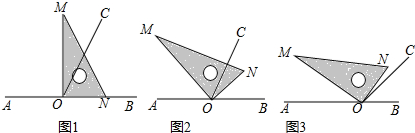
 如图所示是立方体的表面展开图,把它折叠成立方体,它会变成( )
如图所示是立方体的表面展开图,把它折叠成立方体,它会变成( )



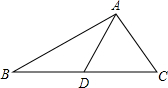 △ABC中,AD为BC边上的中线,已知AB=5,AC=3,求线段AD的长的取值范围.
△ABC中,AD为BC边上的中线,已知AB=5,AC=3,求线段AD的长的取值范围.