题目内容

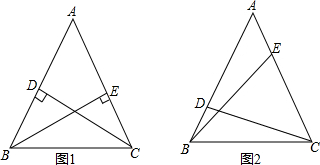
15．如图，已知正方形B的面积为144，正方形C的面积为169时，那么正方形A的面积为（　　）
A．313B．144C．169D．25

分析 由正方形的面积得出EF2=169，DF2=144，在Rt△DEF中，由勾股定理得出DE2=EF2-DF2，即可得出结果．

解答 解：如图所示：
根据题意得：EF2=169，DF2=144，
在Rt△DEF中，由勾股定理得：
DE2=EF2-DF2=169-144=25，
即正方形A的面积为25；
故选：D

点评 本题考查了勾股定理、正方形的性质；熟练掌握正方形的性质，由勾股定理求出DE2是解决问题的关键．

练习册系列答案
相关题目
5．抛物线y=-x2+x+2与y轴的交点坐标是（　　）
A．（1，2）B．（0，-1）C．（0，1）D．（0，2）
6．如图，∠DAC=∠BAC-∠BAD，∠BDC=∠BDA+∠ADC．
3．在-13，0，2，11这四个数中，最小的数是（　　）
A．-13B．0C．2D．11
10．先化简，后求值：
（1）先化简，后求值：3x2y$-[2xy-2（xy-\frac{3}{2}{x}^{2}y）+xy]$，其中x=3，y=-$\frac{1}{3}$
（2）求4x2y-[（4x2y-xyz+3x2z）-3x2z]-2xyz的值，其中负数x的绝对值是2，正数y的倒数是它的本身，负数z的平方等于9．
20．在Rt△ABC中，∠A=30°，∠C=90°，AB+BC=12cm，AB=8cm．
7．解方程：
（1）x2+5x=0
（2）x2-7x+6=0
（3）3x2-8x+4=0                             
（4）$\frac{3}{2}$x2-x+1=0．
4．解方程
（1）（x-3）（x+7）=-9
（2）x2-3x-10=0（配方法解此方程）
13．如图1，在△ABC中，AB=AC，点D，E分别在AB和AC上，且∠ADC=∠AEB=90°，则CD=BE．
探究发现：
如图2，在△ABC中，仍然有条件“AB=AC，点D，E分别在AB和AC上”．若∠ADC+∠AEB=180°，则CD与BE是否仍相等？若相等，请证明；若不相等，请举反例说明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网