Question

16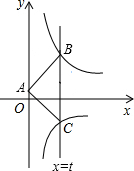．如图，直线x=t（t＞0）与反比例函数y=$\frac{k}{x}$（x＞0）、y=$\frac{-1}{x}$（x＞0）的图象分别交于B、C两点，A为y轴上任意一点，△ABC的面积为3，则k的值为（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 根据点B、C的横坐标，代入反比例函数的解析式求出纵坐标，表示出BC的长，根据三角形面积公式求出k的值．

解答 解：由题意得，点C的坐标（t，-$\frac{1}{t}$），
点B的坐标（t，$\frac{k}{t}$），
BC=$\frac{k}{t}$+$\frac{1}{t}$，
则$\frac{1}{2}$（$\frac{k}{t}$+$\frac{1}{t}$）×t=3，
解得k=5，
故选：D．

点评 本题考查的是反比例函数系数k的几何意义，利用函数解析式表示出点的横纵坐标的关系是解题的关键．