题目内容
1.(1)计算:$\sqrt{8}$-4sin45°.(2)解不等式组$\left\{\begin{array}{l}{x+8<4x-1}\\{\frac{1}{2}x≥4-\frac{3}{2}x}\end{array}\right.$.
分析 (1)由于sin45°=$\frac{\sqrt{2}}{2}$,$\sqrt{8}$利用二次根式的乘法法则化简,然后利用二次根式的加减法则即可求解.
(2)根据不等式的性质求出不等式①和②的解集,根据找不等式组的解集的规律找出不等式组的解集即可.
解答 (1)计算:$\sqrt{8}$-4sin45°.
解:=2$\sqrt{2}$-2$\sqrt{2}$
=0;
(2)解不等式组$\left\{\begin{array}{l}{x+8<4x-1①}\\{\frac{1}{2}x≥4-\frac{3}{2}x②}\end{array}\right.$
解:解①得:x>3,
解②得:x≥2
∴不等式组的解集是x>3.
点评 本题主要考查了特殊角的三角函数值及二次根式的加减法则,解题时首先化简,然后利用二次根式的加减法则计算即可求解,也考查了对解一元一次不等式组等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
16.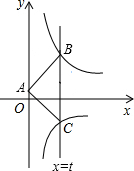 如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
 如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
6.如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
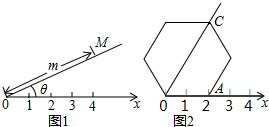

| A. | (60°,4) | B. | (45°,4) | C. | (60°,2) | D. | (50°,2) |
13.某热播视频10天的点击量达51234.8万次,把它用科学记数法表示是( )
| A. | 5.12348×104次 | B. | 0.512348×105次 | C. | 5.12348×108次 | D. | 5.12348×109次 |
 如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).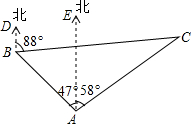 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.
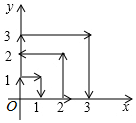 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第28秒时跳蚤所在位置的坐标是(3,5).
一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第28秒时跳蚤所在位置的坐标是(3,5).