题目内容
8.已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0),B1C1∥B2C2∥B3C3,以此继续下去,则点A2015到x轴的距离是$\frac{3}{{2}^{2014}}$.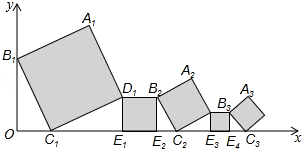
分析 根据勾股定理可得正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,根据相似三角形的性质可得后面正方形的边长依次是前面正方形边长的$\frac{1}{2}$,依次得到第2015个正方形和第2015个正方形的边长,进一步得到点A2015到x轴的距离.
解答 解:如图,∵点C1、E1、E2、C2、E3、E4、C3在x轴上,B1C1∥B2C2∥B3C3,
∴△B1OC1∽△B2E2C2∽B3E4C3…,△B1OC1≌△C1E1D1,…,
∴B2E2=1,B3E4=$\frac{1}{2}$,B4E6=$\frac{1}{4}$,B5E8=$\frac{1}{8}$…,
∴B2015E4017=$\frac{1}{{2}^{2013}}$,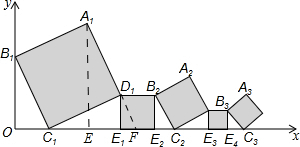
作A1E⊥x轴,延长A1D1交x轴于F,
则△C1D1F∽△C1D1E1,
∴$\frac{{D}_{1}F}{{D}_{1}{E}_{1}}=\frac{{C}_{1}{D}_{1}}{{C}_{1}{E}_{1}}$,
在Rt△OB1C1中,OB1=2,OC1=1,
正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,
∴D1F=$\frac{\sqrt{5}}{2}$,
∴A1F=$\frac{3\sqrt{5}}{2}$,
∵A1E∥D1E1,
∴$\frac{{A}_{1}E}{{D}_{1}{E}_{1}}=\frac{{A}_{1}F}{{D}_{1}F}$,
∴A1E=3,
∴$\frac{{A}_{1}E}{{B}_{1}O}=\frac{3}{2}$,
∴点A2015到x轴的距离是$\frac{1}{{2}^{2013}}×\frac{3}{2}=\frac{3}{{2}^{2014}}$,
故答案为$\frac{3}{{2}^{2014}}$
点评 此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案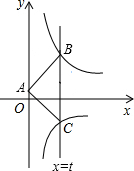 如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 5.12348×104次 | B. | 0.512348×105次 | C. | 5.12348×108次 | D. | 5.12348×109次 |
 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).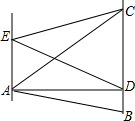 如图所示,直线AE∥BD,点C在BD上,若AE=7,BD=3,△ABD的面积为12,求△ACE的面积.
如图所示,直线AE∥BD,点C在BD上,若AE=7,BD=3,△ABD的面积为12,求△ACE的面积. 如图,已知∠AOB及点E,求作点P,使点P到OA、OB距离相等,且EP=OE.(保留作图痕迹,不写作法,只写结论)
如图,已知∠AOB及点E,求作点P,使点P到OA、OB距离相等,且EP=OE.(保留作图痕迹,不写作法,只写结论)