题目内容
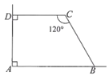
【题目】如图，在
中，对角线
、
交于点
，过点作
，交
延长线于点
，交
于点
，若
，
，
，求
的长.
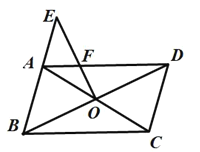
【答案】2
【解析】
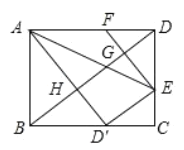
根据平行四边形性质可得到∠ADB=30°，OD=
，进而求出FD，过O作OG∥AB，交AD于G点，易知△AEF∽△GOF，得到
，又因为
，故相似比为1，得到AF=GF，设AF=GF=x，则AD=6+x，又AG=AF+GF=
，列出方程解出x即可.
∵
∴AD∥BC，OD=
∵
∴∠ADB=30°
∵
∴∠DOF=90°
在Rt△ODF中，∠FDO=30°，OD=
∴OF=3，FD=6
如图，过O作OG∥AB，交AD于G点
∴△AEF∽△GOF
∴
∵EF=OF
∴AF=GF
∵O是BD中点
∴G是AD中点
设AF=GF=x，则AD=6+x
∴AG=AF+GF=
∴x+x=
∴x=2
∴AF=2
练习册系列答案
相关题目
