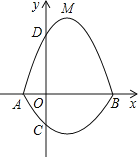题目内容
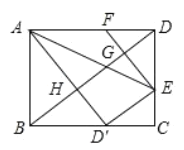
【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点![]() 处,F为AD上一点,且
处,F为AD上一点,且![]() ,EF与BD相交于点G,
,EF与BD相交于点G,![]() 与BD相交于点H,
与BD相交于点H,![]() ,HG=2,则BD=__________.
,HG=2,则BD=__________.
【答案】![]()
【解析】
首先证明出△C![]() E∽△BA
E∽△BA![]() ,然后得出
,然后得出![]() ,进一步再证明△EDF∽△DAB,从而结合题意得出EF⊥BD,然后证明出四边形HGE
,进一步再证明△EDF∽△DAB,从而结合题意得出EF⊥BD,然后证明出四边形HGE![]() 是矩形,得出HG=E
是矩形,得出HG=E![]() =DE=2,之后设EC=y,C
=DE=2,之后设EC=y,C![]() =x,通过△BH
=x,通过△BH![]() ∽△
∽△![]() ,表示出BD,然后再通过△DFE∽△CE
,表示出BD,然后再通过△DFE∽△CE![]() 建立方程求出符合题意的y的值,进而计算求出BD即可.
建立方程求出符合题意的y的值,进而计算求出BD即可.
∵四边形ABCD为矩形,
∴∠B=∠C=90°,
∵∠A![]() E=∠D=90°,
E=∠D=90°,
∴∠A![]() +∠E
+∠E![]() =90°,∠E
=90°,∠E![]() =90°,
=90°,
∴∠A![]() ,
,
∴△C![]() ,
,
∴![]() ,
,
∵C![]() =DF,A
=DF,A![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EDF=∠BAD=90°,
∴△EDF∽△DAB,
∴∠FED=∠ADB,
∵∠ADB+∠BDC=90°,
∴∠FED+∠BDC=90°,
∴EF⊥BD,
又∵![]() ∥BD,A
∥BD,A![]() ,
,
∴BD⊥A![]() ,
,
∴四边形HGE![]() 是矩形,
是矩形,
∴HG=E![]() =DE=2,
=DE=2,
设EC=y,C![]() ,
,
易得△EGD≌△![]() ,
,
∴DG=CE=y,EG=C![]() =H
=H![]() ,
,
∵![]() ∥BD,
∥BD,
∴∠E![]() ,
,
∵∠C=∠BH![]() ,
,
∴△BH![]() ∽△
∽△![]()
∴![]() ,
,
∴![]() ,
,
即BH=![]() ,
,
∴BD=BH+GH+DG=![]() ,
,
易得:△DFE∽△CE![]() ,
,
∴![]()
即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴BD=![]() .
.
所以答案为![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目