��Ŀ����
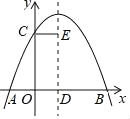
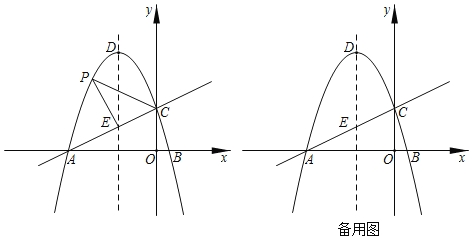
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x+
x+![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣬�����ߵĶԳ�����ֱ��AC���ڵ�E��
��x�ύ��A��B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣬�����ߵĶԳ�����ֱ��AC���ڵ�E��
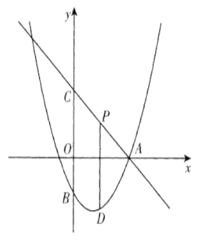
��1������PΪֱ��AC�Ϸ��������ϵĶ��㣬����PC��PE������PCE�����S��PCE���ʱ����P���������߶Գ���ĶԳƵ�Ϊ��Q����ʱ��T�ӵ�Q��ʼ���������ʵ���·���˶���y���ϵĵ�F���������ʵ���·���˶���x���ϵĵ�G����������ʵ���·���˶���ֱ��AC�ϵĵ�H���������������ĵ�P�����꼰QF+FG+![]() AH����Сֵ��
AH����Сֵ��
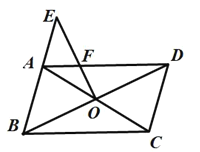
��2������BOC�Ƶ�B˳ʱ����ת120������BO����ֱ����ֱ��AC���ڵ�M����������������CA����ƽ��![]() ����λ����D�Ķ�Ӧ��ΪD������R��y���ϣ���N������ƽ���ڣ����Ե�D����R��M��NΪ������ı���������ʱ����ֱ��д��N�����꣮
����λ����D�Ķ�Ӧ��ΪD������R��y���ϣ���N������ƽ���ڣ����Ե�D����R��M��NΪ������ı���������ʱ����ֱ��д��N�����꣮
���𰸡���1��P����![]() ��
��![]() ����Q'H��
����Q'H��![]() ����2��N����
����2��N����![]() ��
��![]() ����N����
����N����![]() ��
��![]() ����N����
����N����![]() ����
����![]() ����
����
��������
��1������A����3��0����B��1��0����C��0��![]() ����ֱ��AC��ֱ�߽���ʽΪy��
����ֱ��AC��ֱ�߽���ʽΪy��![]() x+
x+![]() ������PCE�����S��PCE���ʱ����P�㵽ֱ��AC�ľ���d��������P���꣬���������Q���꣬����Q����y��ĶԳƵ�Q'����AC����x��ĶԳ�AC'������Q'��ֱ��AC'�Ĵ��߽��ڵ�H����y���ڵ�F����x���ڵ�G��������QF+FG+
������PCE�����S��PCE���ʱ����P�㵽ֱ��AC�ľ���d��������P���꣬���������Q���꣬����Q����y��ĶԳƵ�Q'����AC����x��ĶԳ�AC'������Q'��ֱ��AC'�Ĵ��߽��ڵ�H����y���ڵ�F����x���ڵ�G��������QF+FG+![]() AH����Сֵ��
AH����Сֵ��
��2����ƽ�ƿ�֪�����������ƶ�![]() ����λ������ƽ��1����λ������B'O��ֱ�߽���ʽΪy��
����λ������ƽ��1����λ������B'O��ֱ�߽���ʽΪy��![]() x��
x��![]() ���Ӷ�����֪����M�����꣬Ȼ��������ۣ��ٵ�D'M������RD'NM�ĶԽ���ʱ���ڵ�D'M��RNʱ.
���Ӷ�����֪����M�����꣬Ȼ��������ۣ��ٵ�D'M������RD'NM�ĶԽ���ʱ���ڵ�D'M��RNʱ.
�⣺��1����![]() ����y=0�����
����y=0�����![]() ����A����3��0����B��1��0������x=0�����
����A����3��0����B��1��0������x=0�����![]() ����C��0��
����C��0��![]() �������
������� ��
��
��ֱ��AC��ֱ�߽���ʽΪ![]() ��
��
����P��PK��y�ύAC�ڵ�K���� ������
������![]() ����
����
��![]()

��![]() ��
��
�������߿������£�
�֡�![]() �ҶԳ���Ϊֱ��
�ҶԳ���Ϊֱ��![]()
�൱![]() ʱ��S��PCE���
ʱ��S��PCE���
��
�ߵ�P���������߶Գ���ĶԳƵ�Ϊ��Q�������߶Գ���x����1
��
����Q����y��ĶԳƵ� ������AC����x��ĶԳ�AC'
������AC����x��ĶԳ�AC'
����Q'��ֱ��AC'�Ĵ��߽��ڵ�H����y���ڵ�F����x���ڵ�G��
��Q'F��QF��
�ߡ�CAO����OAH��30�㣬
��HG��AHtan30�㣽![]() AH��
AH��
��QF+FG+![]() AH��Q'F+FG+HG��Q'H��
AH��Q'F+FG+HG��Q'H��
��Q'��Q'M��x�ᣬ��x���ڵ�M����AH�ڵ�N��
��Q'M��![]() ��
��
��Rt��AMN��AM��![]() ��
��
��MN��![]() ��
��
��Q'N��![]() ��
��
��![]() ��
�У�![]()
��![]()
���HQ'N����OAH��30�㣬
��Q'H��![]() ��
��
��2����Rt��OBC��OC��![]() ��OB��1��
��OB��1��
���CBO��60�㣬
�߽���BOC�Ƶ�B˳ʱ����ת120�㣬
���O'BC��60�㣬
��O'��![]() ��
��![]() ����
����
��������������CA����ƽ��![]() ����λ��
�����
��BB'��![]() ��BB'��AC��
��BB'��AC��
���BB'K��30�㣬
����B'��x�ᣬ��x���ڵ�K��
��Rt��BB'K��B'K��![]() ��BK��1��
��BK��1��
�������������ƶ�![]() ����λ������ƽ��1����λ��
����λ������ƽ��1����λ��
��D����1��![]() ����
����
��D'����2��![]() ����
����
��B'O��ֱ�߽���ʽΪy��![]() x��
x��![]() ��
��
M������Ϊ������ �Ľ⣬
�Ľ⣬
��M��![]() ��
��![]() ����
����
�ٵ�D'M������RD'NM�ĶԽ���ʱ��
D'M���е�Ϊ����![]() ��
��![]() ����
����
��R��0��n����N����![]() ��m����
��m����
��![]() ��
��![]() ��
�� ��
��
��m����![]() ��
��
��N����![]() ����
����![]() ����
����
�ڵ�D'M��RNʱ��
��R��0��n����N����![]() ��m����
��m����
��D'M2����![]() ��2+��
��2+��![]() ��2��13��
��2��13��
��D'N2����![]() ��2+��
��2+��![]() ��n��2��13��
��n��2��13��
��m��![]()
![]() ��m��
��m��![]() ��
��![]() ��
��
��N����![]() ��
��![]() ����N����
����N����![]() ��
��![]() ����
����
��N����![]() ��
��![]() ����N����
����N����![]() ��
��![]() ����N����
����N����![]() ����
����![]() ����
����