题目内容
反比例函数y=| k-1 |
| x |
①常数k＜1；
②在每一个象限内，y随x的增大而减小；
③若点A（-l，a）和A′（l，b）都在该函数的图象上，则a+b=0；
④若点B（-2，h）、C（
| 1 |
| 3 |
其中正确的结论的序号是
考点：反比例函数的性质,反比例函数图象上点的坐标特征
专题：
分析：根据反比例函数图象的性质进行判断．
解答：解：①如图所示，双曲线经过第一、三象限，则k-1＞0，即k＞1．故①错误；
②如图所示，在每一个象限内，y随x的增大而减小．故②正确；
③依题意知，-a=b，则a+b=0．故③正确；
④如图所示，在第一象限内，y随x的增大而减小，故n＜m；在第三象限内，y＜0，在第一象限内y＞0．
∵点B在第三象限，点C、D在第一象限，
∴h＜n＜m．
故④错误．
综上所述，正确的结论是②③．
故答案是：②③．
②如图所示，在每一个象限内，y随x的增大而减小．故②正确；
③依题意知，-a=b，则a+b=0．故③正确；
④如图所示，在第一象限内，y随x的增大而减小，故n＜m；在第三象限内，y＜0，在第一象限内y＞0．
∵点B在第三象限，点C、D在第一象限，
∴h＜n＜m．
故④错误．
综上所述，正确的结论是②③．
故答案是：②③．
点评：本题考查了反比例函数的性质，反比例函数图象上点的坐标特征．反比例函数图象上所有点的坐标的横纵坐标的乘积为定值k．
练习册系列答案
相关题目
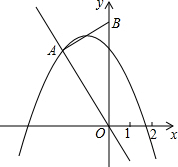在直角坐标系中，点A（-2，4）在经过原点的直线上，过A作直线OA的垂线交y轴于点B．
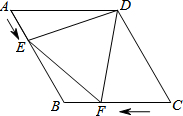如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为
如图，菱形ABCD中，AC∥x轴，点A在反比例函数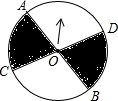
如图，同行转盘中，AB，CD都是直径，圆心角∠AOC=80°，任意旋转这个转盘1次，当旋转停止时，指针指向阴影区域的概率是