题目内容
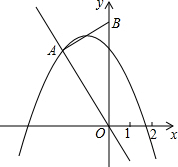 在直角坐标系中,点A(-2,4)在经过原点的直线上,过A作直线OA的垂线交y轴于点B.
在直角坐标系中,点A(-2,4)在经过原点的直线上,过A作直线OA的垂线交y轴于点B.(1)求直线OA的解析式;
(2)求B点坐标;
(3)若抛物线y=a(x+m)2+k的顶点总是落在线段AB上,且它与x轴的一个交点落在(1,0)与(2,0)之间(包括这两点).
当抛物线的顶点A(-2,4),与x轴交于(2,0)时,抛物线开口最大;
当抛物线的顶点B,与x轴交于(
∴a的取值范围是:
考点:二次函数综合题
专题:
分析:(1)设直线OA的解析式为y=kx,将A(-2,4)代入,运用待定系数法即可求出直线OA的解析式;
(2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°,先由同角的余角相等得出∠AOC=∠CAB,再根据两角对应相等的两三角形相似证明△ACB∽△OCA,于是
=
,由此求出BC=1,进而得到B点坐标为(0,5);
(3)将顶点A(-2,4)代入y=a(x+m)2+k,得到y=a(x+2)2+4,再将(2,0)代入,求出抛物线开口最大时的a值;当抛物线的顶点为B时,对称轴为y轴,此时由题意可知当抛物线与x轴交于(1,0),(-1,0)时,抛物线开口最小,求出此时a的值,那么a的取值范围介于这两者之间.
(2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°,先由同角的余角相等得出∠AOC=∠CAB,再根据两角对应相等的两三角形相似证明△ACB∽△OCA,于是
| AC |
| CO |
| BC |
| AC |
(3)将顶点A(-2,4)代入y=a(x+m)2+k,得到y=a(x+2)2+4,再将(2,0)代入,求出抛物线开口最大时的a值;当抛物线的顶点为B时,对称轴为y轴,此时由题意可知当抛物线与x轴交于(1,0),(-1,0)时,抛物线开口最小,求出此时a的值,那么a的取值范围介于这两者之间.
解答:解:(1)设直线OA的解析式为y=kx,
将A(-2,4)代入,得-2k=4,
解得k=-2,
故直线OA的解析式为y=-2x;
 (2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°.
(2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°.
∵∠OAB=90°,
∴∠AOC+∠OAC=90°,∠CAB+∠OAC=90°,
∴∠AOC=∠CAB.
在△ACB与△OCA中,
∴△ACB∽△OCA,
∴
=
,即
=
,
解得BC=1,
∴OB=OC+BC=4+1=5,
∴B点坐标为(0,5);
(3)∵将顶点A(-2,4)代入y=a(x+m)2+k,得到y=a(x+2)2+4,
再将(2,0)代入,得0=a(2+2)2+4,
解得a=-
,此时抛物线开口最大;
当抛物线的顶点为B(0,5)时,解析式为y=ax2+5,
那么当此抛物线与x轴交于(1,0),(-1,0)时,抛物线开口最小,
将(1,0)代入y=ax2+5,得0=a×12+5,
解得a=-5;
∴a的取值范围是:-5<a<-
.
故答案为1,0;-5<a<-
.
将A(-2,4)代入,得-2k=4,
解得k=-2,
故直线OA的解析式为y=-2x;
 (2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°.
(2)过A点作AC⊥y轴于点C,则∠ACB=∠OCA=90°.∵∠OAB=90°,
∴∠AOC+∠OAC=90°,∠CAB+∠OAC=90°,
∴∠AOC=∠CAB.
在△ACB与△OCA中,
|
∴△ACB∽△OCA,
∴
| AC |
| CO |
| BC |
| AC |
| 2 |
| 4 |
| BC |
| 2 |
解得BC=1,
∴OB=OC+BC=4+1=5,
∴B点坐标为(0,5);
(3)∵将顶点A(-2,4)代入y=a(x+m)2+k,得到y=a(x+2)2+4,
再将(2,0)代入,得0=a(2+2)2+4,
解得a=-
| 1 |
| 4 |
当抛物线的顶点为B(0,5)时,解析式为y=ax2+5,
那么当此抛物线与x轴交于(1,0),(-1,0)时,抛物线开口最小,
将(1,0)代入y=ax2+5,得0=a×12+5,
解得a=-5;
∴a的取值范围是:-5<a<-
| 1 |
| 4 |
故答案为1,0;-5<a<-
| 1 |
| 4 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求正比例函数的解析式,相似三角形的判定与性质,二次函数的性质等知识,综合性较强,难度适中.

练习册系列答案
相关题目
以下二次根式:①
;②
;③
;④
中,与
是同类二次根式的是( )
| 12 |
| 22 |
|
| 27 |
| 3 |
| A、①和② | B、②和③ |
| C、①和④ | D、③和④ |
 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系,A(3,2),B(6,2),C(3,0).
如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系,A(3,2),B(6,2),C(3,0).
 如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.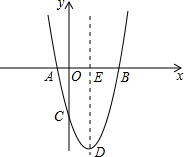 已知抛物线l1:y=ax2-2ax+b与x轴交于A、B两点,与y轴负半轴交于点C,且A(-1,0),OB=OC
已知抛物线l1:y=ax2-2ax+b与x轴交于A、B两点,与y轴负半轴交于点C,且A(-1,0),OB=OC  反比例函数y=
反比例函数y=