题目内容
9.先化简,再求值:($\frac{m+2}{m}$-$\frac{m-1}{m-2}$)$÷\frac{m-4}{{m}^{2}-4m+4}$,其中m是不等式3m-1>-7的负整数解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式的解集确定出负整数解m的值,代入计算即可求出值.
解答 解:原式=$\frac{(m+2)(m-2)-m(m-1)}{m(m-2)}$•$\frac{(m-2)^{2}}{m-4}$=$\frac{m-4}{m(m-2)}$•$\frac{(m-2)^{2}}{m-4}$=$\frac{m-2}{m}$,
由3m-1>-7,解得:m>-2,即不等式的负整数解为m=-1,
则原式=3.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
4.要调查姜堰城区八年级5000名学生了解“溱潼会船节”的情况,下列调查方式最合适的是( )
| A. | 在某校八年级选取100名女生 | |
| B. | 在某校八年级选取100名男生 | |
| C. | 在某校八年级选取100名学生 | |
| D. | 在城区5000名八年级学生中随机选取100名学生 |
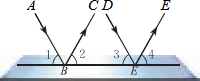 如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.
如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.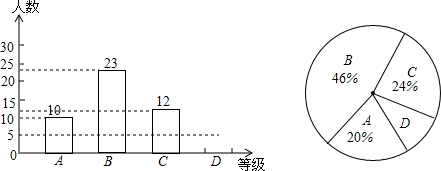
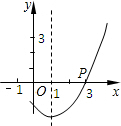 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论: 如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.
如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.