题目内容
11.先化简,再求值:已知a2+2a-2=0,求代数式($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$的值.
分析 先根据分式混合运算的法则把原式进行化简,再根据a2+2a-2=0得出a2+2a=2,代入分式进行检验即可.
解答 解:原式=[$\frac{a-2}{a(a+2)}$-$\frac{a-1}{(a+2)^{2}}$]•$\frac{a+2}{a-4}$
=[$\frac{(a-2)(a+2)}{a(a+2)^{2}}$-$\frac{a(a-1)}{a(a+2)^{2}}$]•$\frac{a+2}{a-4}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{a(a+2)^{2}}$•$\frac{a+2}{a-4}$
=$\frac{1}{a(a+2)}$
=$\frac{1}{{a}^{2}+2a}$,
∵a2+2a-2=0,
∴a2+2a=2,
∴原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{16}$=4 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{-64}$=4 | D. | (2$\sqrt{3}$)2=6 |
 如图是由正方形ABCD和直角梯形DEFC组成的图形,已知正方形ABCD的面积为100,求阴影部分面积?
如图是由正方形ABCD和直角梯形DEFC组成的图形,已知正方形ABCD的面积为100,求阴影部分面积?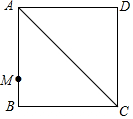 如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值.
如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值.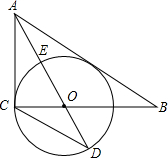 如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.