题目内容
2. 如图是由正方形ABCD和直角梯形DEFC组成的图形,已知正方形ABCD的面积为100,求阴影部分面积?
如图是由正方形ABCD和直角梯形DEFC组成的图形,已知正方形ABCD的面积为100,求阴影部分面积?
分析 利用等积变换思想,将所求阴影部分面积转化成一个规则的易求的几何图形的面积.首先,△GCF的面积等于△GCE的面积,而△BCE的面积等于△ABC的面积.
解答 解:如图,连接CE.
∵CD∥EF,
∴S△GCF=S△GCE,
∵AE∥BC,
∴${S}_{△BCE}={S}_{△ABC}=\frac{1}{2}{S}_{ABCD}$=50,
即阴影部分的面积为50.
点评 本题主要考查了三角形面积的等积变换,难度不大,但却是一道经典好题.巧妙地将所求阴影部分的面积转化成△ABC的面积是解决本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10.近似数8.1754精确百分位,正确的是( )
| A. | 8.2 | B. | 8.17 | C. | 8.18 | D. | 8.175 |
14.抛物线y=-2x2先向左平移1个单位,再向下平移3个单位,所得抛物线是( )
| A. | y=-2 (x+1)2+3 | B. | y=-2 (x+1)2-3 | C. | y=-2 (x-1)2-3 | D. | y=-2 (x-1)2+3 |
 观察图给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n个点阵中的点的个数s为4n-3.
观察图给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n个点阵中的点的个数s为4n-3. 如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为( )
如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为( )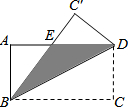 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,求图中阴影部分的面积.
如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,求图中阴影部分的面积.