题目内容
3.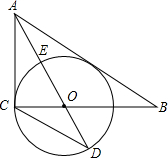 如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,AE:AC=1:2,⊙O的半径为3,求AE的长.
(3)在(2)的条件下,延长AO交⊙O于点D,求△ACD的面积.
分析 (1)作OF⊥AB于F,如图,先根据角平分线的性质定理得到OF=OC,然后根据切线的判定定理可判断AB是⊙O的切线;
(2)设AE=x,则AC=2x,利用勾股定理得到32+(2x)2=(x+3)2,然后解方程求出x即可得到AE的长;
(3)作CH⊥OA于H,如图,利用面积法求出CH,然后根据三角形面积公式计算△ACD的面积.
解答 (1)证明:作OF⊥AB于F,如图,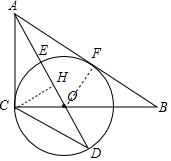
∵AO是∠ABC的角平分线,
而OC⊥AC,OF⊥AB,
∴OF=OC,
而OC为圆的半径,
∴AB是⊙O的切线;
(2)解:设AE=x,则AC=2x,
在Rt△AOC中,∵OC2+AC2=OA2,
∴32+(2x)2=(x+3)2,解得x1=0(舍去),x2=2,
∴AE=2;
(3)作CH⊥OA于H,如图,
∵$\frac{1}{2}$CH•OA=$\frac{1}{2}$AC•OC,
∴CH=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴△ACD的面积=$\frac{1}{2}$•AD•CH=$\frac{1}{2}$×8×$\frac{12}{5}$=$\frac{48}{5}$.
点评 本题考查了圆的综合题:熟练掌握切线的判定方法和角平分线的性质定理;会运用勾股定理计算线段的长.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
14.抛物线y=-2x2先向左平移1个单位,再向下平移3个单位,所得抛物线是( )
| A. | y=-2 (x+1)2+3 | B. | y=-2 (x+1)2-3 | C. | y=-2 (x-1)2-3 | D. | y=-2 (x-1)2+3 |
 观察图给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n个点阵中的点的个数s为4n-3.
观察图给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n个点阵中的点的个数s为4n-3.
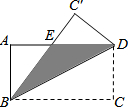 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,求图中阴影部分的面积.
如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,求图中阴影部分的面积. 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于D、E,交
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于D、E,交