题目内容
14．△ABC中，AB=15，BC=14，AC=13，则△ABC的面积是（ ）| A． | 96 | B． | 120 | C． | 84 | D． | 60 |
分析 过点A作AD⊥BC，利用勾股定理求出AD的长，再利用三角形的面积公式求出△ABC的面积即可．
解答 
解：设BD=x，则CD=14-x，在Rt△ABD中，AD2+x2=132，
在Rt△ADC中，AD2=152-（14-x）2，
∴132-x2=152-（14-x）2，
132-x2=152-196+28x-x2，
解得x=9，
∴CD=5，
在Rt△ACD中，AD=$\sqrt{1{3}^{2}-{5}^{2}}$=12，
∴△ABC的面积=$\frac{1}{2}$×BC•AD=$\frac{1}{2}$×14×12=84，
故选C．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
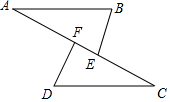点A、F、E、C在同一条直线上，①AF=CE，②BE=DF，③BE∥DF，④∠A=∠C．请你从这四个条件中选出三个作为条件，另一个作为结论，组成一个真命题，并给予证明．
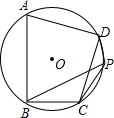已知四边形ABCD内接于⊙O，∠D=90°，P为$\widehat{CD}$上一动点（不与点C，D重合）．
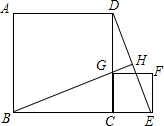已知，如图所示，正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．求证：
如图，在△ABC中，AC=BC，∠BAC=30°，D是EF的中点，E是线段BC延长线上一点，过点A作AF∥BE，与线段ED的延长线交于点F，连结AE、CF．