��Ŀ����
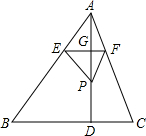 ��֪�������������ֽƬABC�У�ֱ��EF��BC����ֽƬ��ֱ��EF�۵����ֱ��߶�AB��AC��AD��E��F��G�����A����ƽ���ϵĵ�ΪP������E��F��PΪ����������Ρ�EFP��Ϊ��AEF�ġ��۵������Ρ����������������ֽƬABC�У�BC=4����AD=3��EF=x��
��֪�������������ֽƬABC�У�ֱ��EF��BC����ֽƬ��ֱ��EF�۵����ֱ��߶�AB��AC��AD��E��F��G�����A����ƽ���ϵĵ�ΪP������E��F��PΪ����������Ρ�EFP��Ϊ��AEF�ġ��۵������Ρ����������������ֽƬABC�У�BC=4����AD=3��EF=x����1����ͼ�����߶�AG�ij�����x�Ĵ���ʽ��ʾ����
��2����ֽƬ��ֱ��EF�۵������A����ƽ���ϵĵ�ΪP����AEF�ġ��۵������Ρ���PEF���ı���BCFE�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
���㣺���۱任���۵����⣩
ר�⣺������
��������1��֤����AEF�ס�ABC���������Ʊȼ��ɵõ�AG=
x��
��2���ȸ����۵��õ�PG=AG=
x���ٷ������ۣ���P���ڡ�ABC���ڲ�����ͼ1����x��2����ʱy=S��AEF�����������������ʽ�õ�y=
x2����P���ڡ�ABC���ⲿ����ͼ2��PE��PF�ֱ�BC��M��N�㣬�ȱ�ʾ��PG=AG=
x��PA=2AG=
x��PD=PA-AD=
x-3��DG=AD-AG=3-
x����֤����PMN�ס�PEF���������Ʊȱ�ʾ��MN=2x-4����ʱy=S����MNFE���������ε������ʽ�õ�y=-
x2+6x-6��2��x��3����
| 3 |
| 4 |
��2���ȸ����۵��õ�PG=AG=
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
��� �⣺��1����EF��BC��
�⣺��1����EF��BC��
���AEF�ס�ABC��
��
=
����
=
��
��AG=
x��0��x��3����
��2���������Ρ�EFP��Ϊ��AEF�ġ��۵������Ρ���
��PG=AG��
��P���ڡ�ABC���ڲ�����ͼ1����AP��AD����2•
x��3�����x��2����ʱy=S��AEF=
EF•AG=
•x•
x=
x2��
��P���ڡ�ABC���ⲿ����ͼ2��PE��PF�ֱ�BC��M��N�㣬��PG=AG=
x��PA=2AG=
x��PD=PA-AD=
x-3��DG=AD-AG=3-
x��
��MN��EF��
���PMN�ס�PEF��
��
=
����
=
��
��MN=2x-4��
��y=S����MNFE=
��MN+EF��•DG
=
��2x-4+x��•��3-
x��
=-
x2+6x-6��2��x��3����
����������y����x�ĺ�����ϵΪ��y=
��
 �⣺��1����EF��BC��
�⣺��1����EF��BC�����AEF�ס�ABC��
��
| AG |
| AD |
| EF |
| BC |
| AG |
| 3 |
| x |
| 4 |
��AG=
| 3 |
| 4 |
��2���������Ρ�EFP��Ϊ��AEF�ġ��۵������Ρ���
��PG=AG��
��P���ڡ�ABC���ڲ�����ͼ1����AP��AD����2•
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
��P���ڡ�ABC���ⲿ����ͼ2��PE��PF�ֱ�BC��M��N�㣬��PG=AG=
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |

��MN��EF��
���PMN�ס�PEF��
��
| MN |
| EF |
| PD |
| PG |
| MN |
| x |
| ||
|
��MN=2x-4��
��y=S����MNFE=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 4 |
=-
| 9 |
| 8 |
����������y����x�ĺ�����ϵΪ��y=
|
���������⿼�����۵������ʣ��۵���һ�ֶԳƱ任����������Գƣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͶ�Ӧ����ȣ�Ҳ���������������ε��ж������ʣ�

��ϰ��ϵ�д�
�����Ŀ

 ������ͼ��
������ͼ��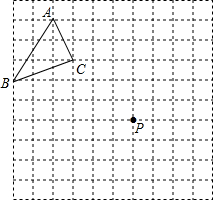 ��ͼ�����������С�ABC������Aƽ�Ƶ���P��������ABCƽ�ƺ��ͼ�Σ�
��ͼ�����������С�ABC������Aƽ�Ƶ���P��������ABCƽ�ƺ��ͼ�Σ�