题目内容
8.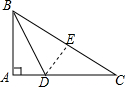 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.
分析 过点D作DE⊥BC于E,根据根据勾股定理求得AD,再根据角平分线上的点到角的两边距离相等可得DE=AD,即可得到结论.
解答  解:过D作DE⊥BC于E,
解:过D作DE⊥BC于E,
∵BD平分∠ABC交AC于点D,∠A=90°,
∴DE=AD,
∵AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{3}^{2}-(\sqrt{5})^{2}}$=4,
∴DE=AD=4.
故答案为:4.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法中,正确的是( )
| A. | 1的平方根是1 | B. | -1是1的平方根 | C. | 8的立方根是±2 | D. | $\sqrt{9}$=±3 |
17.$\frac{1}{2}$是一个数的算术平方根,则这个数为( )
| A. | 4 | B. | 1 | C. | $\frac{1}{4}$ | D. | ±$\frac{1}{4}$ |
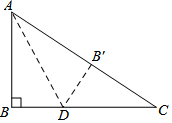 如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上得到线段AB',折痕为AD,则BD的长为3.
如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上得到线段AB',折痕为AD,则BD的长为3.
 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的三等分线交于点P、Q,求∠P+∠Q.(用含m的式子表示)
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的三等分线交于点P、Q,求∠P+∠Q.(用含m的式子表示) 如图,点C,D在线段AB上,且△PCD是等边三角形.
如图,点C,D在线段AB上,且△PCD是等边三角形. 如图,已知直线AB上一点O,∠AOD=42°,∠BOC=34°,∠DOE=90°,OF平分∠COD,求∠FOD与∠EOB的度数.
如图,已知直线AB上一点O,∠AOD=42°,∠BOC=34°,∠DOE=90°,OF平分∠COD,求∠FOD与∠EOB的度数.