题目内容
3. 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的三等分线交于点P、Q,求∠P+∠Q.(用含m的式子表示)
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的三等分线交于点P、Q,求∠P+∠Q.(用含m的式子表示)
分析 由三角形的外角性质可得出∠ACD-∠ABC=∠A=m°、∠P=∠PCD-∠PBC、∠Q=∠QCD-∠QBC,再根据∠ABC和∠ACD的三等分线交于点P、Q,即可得出∠P、∠Q的度数,将其相加即可得出结论.
解答 解:∵∠A+∠ABC=∠ACD,
∴∠ACD-∠ABC=∠A=m°.
∵∠ABC和∠ACD的三等分线交于点P、Q,
∴∠P=∠PCD-∠PBC=$\frac{2}{3}$(∠ACD-∠ABC)=$\frac{2}{3}$m°,
∠Q=∠QCD-∠QBC=$\frac{1}{3}$(∠ACD-∠ABC)=$\frac{1}{3}$m°,
∴∠P+∠Q=$\frac{2}{3}$m°+$\frac{1}{3}$m°=m°.
点评 本题考查了三角形的外角性质以及角平分线的定义,根据三角形的外角性质结合角三等分线的定义找出∠P、∠Q的度数是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
13.下列四组线段中,能构成直角三角形的是( )
| A. | 9,12,13 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 32,42,52 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
11.若x=2是方程x2-mx-6=0的一个解,则m的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 2 |
13. 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是( )
如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是( )
 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是( )
如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是( )| A. | ∠1+∠2=180° | B. | ∠1+∠2=90° | C. | ∠1=∠2 | D. | 无法确定 |
 如图,延长?ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A、E和C、F.求证:AE=CF.
如图,延长?ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A、E和C、F.求证:AE=CF.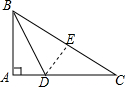 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.