题目内容
20. 如图,点C,D在线段AB上,且△PCD是等边三角形.
如图,点C,D在线段AB上,且△PCD是等边三角形.(1)当AC,CD,DB满足怎样的数量关系时,△ACP∽△PDB,说明你的理由.
(2)当△ACP∽△PDB时,求∠APB的度数.
分析 (1)根据等边三角形的性质得到∠PCD=∠PDC=60°,PC=CD=PD,根据外角的性质得到∠ACP=∠PDB=120°,然后根据相似三角形的判定即可得到结论;
(2)根据相似三角形的性质得到∠APC=∠PBD,根据外角的性质得到∠DPB+∠DBP=60°,于是得到结论.
解答 解:(1)当CD2=AC•DB时,△ACP∽△PDB,
∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PC=CD=PD,
∴∠ACP=∠PDB=120°,
∵CD2=AC•DB,
∴$\frac{CD}{BD}$=$\frac{AC}{CD}$,即$\frac{PC}{BD}$=$\frac{AC}{PD}$,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD,
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠CPD+∠APC+∠BPD=120°.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
11.若x=2是方程x2-mx-6=0的一个解,则m的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 2 |
5.若|a+9|+(b-8)2=0,则(a+b)2016的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.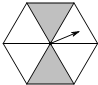 如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
 如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
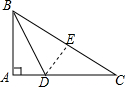 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=$\sqrt{5}$,BD=3,则点D到BC的距离DE是4.