题目内容
任意抛掷一枚均匀的骰子两次,当骰子停止运动后朝上一面的数分别记为a,b,则关于x、y的方程组
有正整数解的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法,解二元一次方程组
专题:
分析:首先列举出a,b所有的可能结果,然后求出有正数解时,所有的可能,进而求出概率.
解答:解:∵第一次掷出的点数为a,第二次掷出的点数为b,
∴所有的可能如图所示:
∵要使关于x,y的方程组
有正数解,符合要求的只有3组,(3,2),(4,4),(5,6),
∴有正数解的概率为
=
.
故选B.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1,1, | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| 2 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
| 5 | 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
| 6 | 6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
∵要使关于x,y的方程组
|
∴有正数解的概率为
| 3 |
| 36 |
| 1 |
| 12 |
故选B.
点评:此题考查了列表法与树状图法;用到的知识点为:概率=所求情况数与总情况数之比,关键是求出方程组的正整数解.

练习册系列答案
相关题目
小青进行打靶训练,需射击10次,在第6、第7、第8、第9次射击中,分别得了9.0环、8.4环、8.1环、9.3环.他前9次射击所得的平均环数高于前5次射击环数的平均环数.如果他要使10次射击的平均环数超过8.8环,那么他在第10次射击时击中环数至少是(每次射击所得环数都精确到0.1环)( )
| A、9.9 | B、9.8 |
| C、9.6 | D、10 |
已知a(b+2)是一个不为0的常数,且当a=2时,b=1;那么当b=4时,a=( )
| A、1 | B、2 | C、3 | D、4 |
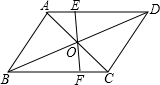 如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有( )
如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有( )