题目内容
小青进行打靶训练,需射击10次,在第6、第7、第8、第9次射击中,分别得了9.0环、8.4环、8.1环、9.3环.他前9次射击所得的平均环数高于前5次射击环数的平均环数.如果他要使10次射击的平均环数超过8.8环,那么他在第10次射击时击中环数至少是(每次射击所得环数都精确到0.1环)( )
| A、9.9 | B、9.8 |
| C、9.6 | D、10 |
考点:一元一次不等式组的应用
专题:
分析:首先设前5次平均分为x,利用他前9次射击所得的平均环数高于前5次射击环数的平均环数,以及第6、第7、第8、第9次射击中,分别得了9.0环、8.4环、8.1环、9.3环.得出x的取值范围,进而得出5x最大值,故可求出第10次射击至少得的环数.
解答:解:由题设知,设前5次平均分为x,利用他前9次射击所得的平均环数高于前5次射击环数的平均环数,
得出:
>x,
解得:x<8.7,
要使10次射击的平均环数超过8.8环,设第10次射击时击中环数至少是y,
则(5x+9.0+8.4+8.1+9.3+y)÷10>8.8,
∵5x最大值为5×8.7-0.1=43.4,
∴(43.4+9.0+8.4+8.1+9.3+y)÷10>8.8,
解得:y>9.8.
∴他在第10次射击时击中环数至少是:9.9环.
故选:A.
得出:
| 5x+9.0+8.4+8.1+9.3 |
| 9 |
解得:x<8.7,
要使10次射击的平均环数超过8.8环,设第10次射击时击中环数至少是y,
则(5x+9.0+8.4+8.1+9.3+y)÷10>8.8,
∵5x最大值为5×8.7-0.1=43.4,
∴(43.4+9.0+8.4+8.1+9.3+y)÷10>8.8,
解得:y>9.8.
∴他在第10次射击时击中环数至少是:9.9环.
故选:A.
点评:本题考查的是一元一不等式的应用以及最值应用.得出前5次射击环数的最大值是解决本题的关键.

练习册系列答案
相关题目
已知|a|>a,|b|>b,且|a|>|b|,则a、b的大小关系为( )
| A、a>b | B、a=b |
| C、a<b | D、无法确定 |
任意抛掷一枚均匀的骰子两次,当骰子停止运动后朝上一面的数分别记为a,b,则关于x、y的方程组
有正整数解的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB∥CD,BE⊥EF于E,∠EFD=60°,∠B的度数是( )
如图,AB∥CD,BE⊥EF于E,∠EFD=60°,∠B的度数是( )| A、80° | B、60° |
| C、45° | D、30° |
某个星期中,从周一到周五这五天的日历号数之和为70,则这一周的星期六的日历号数是( )
| A、15 | B、16 | C、17 | D、18 |




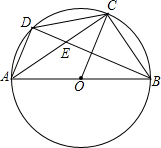 如图,已知△ABC内接于圆O,AB是直径,D是AC弧上的点,BD交AC于E,AB=5,sin∠CAB=
如图,已知△ABC内接于圆O,AB是直径,D是AC弧上的点,BD交AC于E,AB=5,sin∠CAB=