题目内容
若(x+1)2+(x-3)2=16,则(3-x)2(1+x)2= .
考点:完全平方公式
专题:计算题
分析:分别把(x+1)、(x-3)看作一个整体,求出这两个数的差的平方,然后求出乘积二倍项,再平方即可.
解答:解:[(x+1)-(x-3)]2=(x+1)2+2(x-3)(1+x)+(x-3)2,
即(x+1-x+3)2=16+2(x-3)(1+x)=42,
解得(x-3)(1+x)=0,
所以(3-x)2(1+x)2=0.
故答案为:0.
即(x+1-x+3)2=16+2(x-3)(1+x)=42,
解得(x-3)(1+x)=0,
所以(3-x)2(1+x)2=0.
故答案为:0.
点评:本题主要考查完全平方公式的变形,熟记公式结构是解题的关键.完全平方公式:(a±b)2=a2±2ab+b2.

练习册系列答案
相关题目
任意抛掷一枚均匀的骰子两次,当骰子停止运动后朝上一面的数分别记为a,b,则关于x、y的方程组
有正整数解的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、等腰梯形、菱形、正五边形的图案,你认为符合要求的是( )
| A、正三角形 | B、等腰梯形 |
| C、菱形 | D、正五边形 |
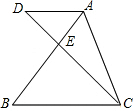 如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于
如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于