题目内容
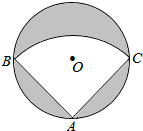 如图,有一直径是
如图,有一直径是| 2 |
(1)求AB的长;
(2)求图中阴影的面积;
(3)若用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
考点:扇形面积的计算,圆锥的计算
专题:
分析:(1)根据圆周角定理由∠BAC=90°得BC为⊙O的直径,即BC=
,根据等腰直角三角形的性质得AB=1;
(2)用圆的面积减去扇形的面积即可求解;
(3)由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,则2πr=
,然后解方程即可.
| 2 |
(2)用圆的面积减去扇形的面积即可求解;
(3)由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,则2πr=
| 90π×1 |
| 180 |
解答:解:(1)∵∠BAC=90°,
∴BC为⊙O的直径,即BC=
,
∴AB=
BC=1;
(2)S阴影=S圆-S扇形=π(
)2-
=
;
(3)设所得圆锥的底面圆的半径为r,
根据题意得2πr=
,
解得r=
.
∴BC为⊙O的直径,即BC=
| 2 |
∴AB=
| ||
| 2 |
(2)S阴影=S圆-S扇形=π(
| ||
| 2 |
| 90π×12 |
| 360 |
| π |
| 4 |
(3)设所得圆锥的底面圆的半径为r,
根据题意得2πr=
| 90π×1 |
| 180 |
解得r=
| 1 |
| 4 |
点评:本题考查了扇形的面积计算以及圆锥的计算,解答本题的关键是掌握扇形的面积公式:
.
| nπR2 |
| 360 |

练习册系列答案
相关题目
下列各式正确的是( )
| A、cos60°<sin45°<tan45° |
| B、sin45°<cos60°<tan45° |
| C、sin45°<tan45°<cos60 |
| D、cos60°<tan45°<sin45° |
在△ABC中,∠B的平分线与∠C的平分线相交于O,且∠BOC=130°,则∠A=( )
| A、50° | B、60° |
| C、80° | D、100° |
已知0<x<3,化简
-
的结果是( )
| (2x+1)2 |
| x2-10x+25 |
| A、3x-4 | B、x-4 |
| C、3x+6 | D、-x+6 |
 如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是
如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是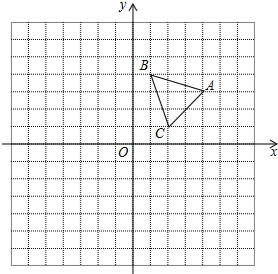 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,3)、B(1,4)、C(2,1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,3)、B(1,4)、C(2,1).