题目内容
10. 如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.
如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.
分析 根据垂直的定义得到∠ACB=∠ADC=90°,推出△ACD∽△ABC,根据相似三角形的性质得到$\frac{AC}{AD}=\frac{AB}{AC}$,同时代的AC2AD•AB,由于AB=AF+FB,等量代换得AC2=AD•(AF+FB)=AD•AF+AD•FB 通过△ACD∽△BEF,根据形式是三角形的性质得到$\frac{AD}{CD}=\frac{EF}{FB}$,于是得到AD•FB=CD•EF,即可得到结论.
解答 证明:∵CD是Rt△ABC的斜边AB上的高,
∴∠ACB=∠ADC=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AD}=\frac{AB}{AC}$,
∴AC2AD•AB,
∵AB=AF+FB,
∴AC2=AD•(AF+FB)=AD•AF+AD•FB,
∵EF⊥AB于点F,
∴∠ADC=∠EFB=90°,
∴∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△BEF,
∴$\frac{AD}{CD}=\frac{EF}{FB}$,
∴AD•FB=CD•EF,
∴AC2=AD•AF+AD•FB=AD•AF+CD•FB.
点评 本题考查了相似三角形的判定和性质,垂直的定义,余角的性质,证得△ACD∽△BEF是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
18.某化肥厂把化肥送到甲、乙两个村庄,先后各送了两次.每次的运量和运费如表
试问两个村庄应该各负担运费多少元?(提醒:一吨化肥运往同一村庄的运费相同.)
| 次序 | 甲村运量(吨) | 乙村运量(吨) | 共计运费(元) |
| 第1次 | 6 | 5 | 270 |
| 第2次 | 8 | 11 | 490 |
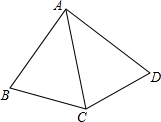 如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由. 已知,∠α,线段a、b,求作△ABC,使图∠C=∠α,BC=a,AC=b(尺规作图)
已知,∠α,线段a、b,求作△ABC,使图∠C=∠α,BC=a,AC=b(尺规作图)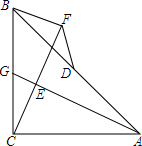 等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF.
等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF.