题目内容
5.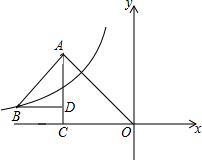 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第二象限经过点B,若OA2-AB2=24,则k的值为-12.
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第二象限经过点B,若OA2-AB2=24,则k的值为-12.
分析 设B点坐标为(a,b),根据等腰直角三角形的性质得OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,则OA2-AB2=24变形为AC2-AD2=12,利用平方差公式得到(AC+AD)(AC-AD)=12,所以(OC+BD)•CD=12,则有a•b=-12,根据反比例函数图象上点的坐标特征易得k=-12.
解答 解:设B点坐标为(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,
∵OA2-AB2=24,
∴2AC2-2AD2=24,即AC2-AD2=12,
∴(AC+AD)(AC-AD)=12,
∴(OC+BD)•CD=12,
∴a•b=-12,
∴k=-12.
故答案为:-12.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
20.用配方法解方程x2+6x+1=0,配方后的方程是( )
| A. | (x+3)2=8 | B. | (x-3)2=8 | C. | (x-3)2=10 | D. | (x+3)2=10 |
17.不能判定两个三角形全等的是( )
| A. | 三条边对应相等 | B. | 两条边及其夹角对应相等 | ||
| C. | 两角和一条边对应相等 | D. | 两条边和一条边所对的角对应相等 |
14.如果一个多边形的每个内角都是120°,那么这个多边形是( )
| A. | 三角形 | B. | 六边形 | C. | 七边形 | D. | 九边形 |