题目内容
2.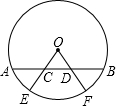 如图,已知⊙0的弦AB,E,F是弧AB上两点,$\widehat{AE}$=$\widehat{BF}$,OE、OF分别交于AB于C、D两点,求证:AC=BD.
如图,已知⊙0的弦AB,E,F是弧AB上两点,$\widehat{AE}$=$\widehat{BF}$,OE、OF分别交于AB于C、D两点,求证:AC=BD.
分析 连接OA、OB,根据半径相等得到∠A=∠B,根据等弧所对的圆周角相等得到∠AOC=∠BOD,根据三角形全等的判定定理证明△AOC≌△BOD,根据全等三角形的性质证明结论.
解答 证明: 连接OA、OB,
连接OA、OB,
∵OA=OB,
∴∠A=∠B,
∵$\widehat{AE}$=$\widehat{BF}$,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
$\left\{\begin{array}{l}{∠A=∠B}\\{OA=OB}\\{∠AOC=∠BOD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD.
点评 本题考查的是圆心角、弧、弦的关系以及三角形全等的判定和性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.

练习册系列答案
相关题目
13.已知一次函数y=kx+b的图象与直线y=-x+1平行,且过点(1,-2),那么此一次函数的解析式为( )
| A. | y=-x+1 | B. | y=x-1 | C. | y=x+2 | D. | y=-x-1 |
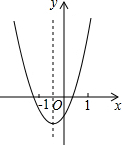 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )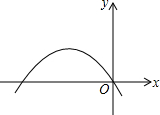 如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).
如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).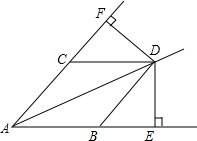 已知如图,点B、C在∠A的两边上,且AB=AC,D为∠CAB内的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.
已知如图,点B、C在∠A的两边上,且AB=AC,D为∠CAB内的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.