题目内容
8.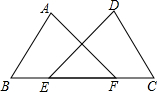 如图,点E,F在BC上,AB=DC,∠A=∠D,∠B=∠C.求证:BE=FC.
如图,点E,F在BC上,AB=DC,∠A=∠D,∠B=∠C.求证:BE=FC.
分析 只要证明△ABF≌△DCE(ASA),推出BF=CE,再根据线段的和差定义即可证明.
解答 证明:在△ABF与△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AB=DC}\\{∠B=∠C}\end{array}\right.$,
∴△ABF≌△DCE(ASA),
∴BF=CE,
∴BF-EF=CE-EF,
∴BE=CF.
点评 本题考查全等三角形的判定和性质,解题的关键是熟练掌握所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.在平面直角坐标系中,已知点A(0,1),B(4,2),以原点O为位似中心,把△OAB按相似比1:2缩小,则点B的对应点B′的坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (2,1)或(-2,1) | D. | (2,1)或(-2,-1) |
16.若分式$\frac{3x-6}{2x+1}$的值为0,则x的值为( )
| A. | 2 | B. | 3 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{2}$或2 |
17.对于函数y=-2x+4.下列说法错误的是( )
| A. | y随x的增大而减小 | B. | 它的图象与y轴的交点是(0,4) | ||
| C. | 当x<2时,y<0 | D. | 它的图象不经过第三象限 |
18. 一副三角板如图叠放在一起,∠α的度数为( )
一副三角板如图叠放在一起,∠α的度数为( )
 一副三角板如图叠放在一起,∠α的度数为( )
一副三角板如图叠放在一起,∠α的度数为( )| A. | 95° | B. | 100° | C. | 105° | D. | 120° |
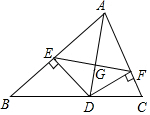 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )