题目内容
3.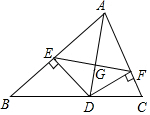 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据角平分线性质求出DE=DF,证△AED≌△AFD,推出AE=AF,再逐个判断即可.
解答 解:∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,∠ADE=∠ADF,
∴AD平分∠EDF;③正确;
∵AD平分∠BAC,
∵AE=AF,DE=DF,
∴AD垂直平分EF,①正确;②错误,
∵∠BAC=60°,
∴∠DAG=30°,
∴AG=$\frac{\sqrt{3}}{2}$AE,AD=$\frac{2\sqrt{3}}{3}$AE,
∴DG=$\frac{\sqrt{3}}{6}$AE,
∴AG=3DG,④正确.
故选A.
点评 本题考查了全等三角形的性质和判定,正方形的判定,角平分线性质的应用,能求出Rt△AED≌Rt△AFD是解此题的关键.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | a6÷a2=a3 | B. | (a2)3=a5 | C. | a0=0 | D. | a-3=$\frac{1}{{a}^{3}}$ |
13.对整式3x2-12y2因式分解正确的是( )
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
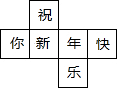 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“快”相对的面上的汉字是新.
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“快”相对的面上的汉字是新.
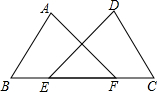 如图,点E,F在BC上,AB=DC,∠A=∠D,∠B=∠C.求证:BE=FC.
如图,点E,F在BC上,AB=DC,∠A=∠D,∠B=∠C.求证:BE=FC. 如图,某校要在长为32m,宽为20m的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为540m2,求道路的宽.
如图,某校要在长为32m,宽为20m的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为540m2,求道路的宽.