题目内容
10.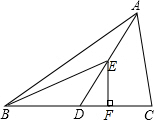 如图,△ABC的面积为40,AD为△ABC的中线,BD=5,BE为△ABD的中线,
如图,△ABC的面积为40,AD为△ABC的中线,BD=5,BE为△ABD的中线,EF⊥BC,则点E到BC边的距离为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
分析 因为S△ABD=$\frac{1}{2}$S△ABC、S△BDE=$\frac{1}{2}$S△ABD;所以S△BDE=$\frac{1}{4}$S△ABC,再根据三角形的面积公式求得即可.
解答 解:∵AD是△ABC的中线,BC=10,
∴S△ABD=$\frac{1}{2}$S△ABC,BD=5;
同理,BE是△ABD的中线,S△BDE=$\frac{1}{2}$S△ABD;
∴S△BDE=$\frac{1}{4}$S△ABC,
∵S△BDE=$\frac{1}{2}$BD•EF,
∴$\frac{1}{2}$BD•EF=$\frac{1}{4}$S△ABC,
又∵△ABC的面积为40,BD=5,
∴EF=4,
故选C.
点评 此题考查了三角形的面积,要理解三角形高的定义,根据三角形的面积公式求解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
1.下列方程中,是一元二次方程的有( )个.
①ax2+bx+c=0;②2x(x-3)=2x2+1;③x2=4;④(2x)2=(x-1)2 ⑤$\frac{{x}^{2}-3x}{x}$=2x2.
①ax2+bx+c=0;②2x(x-3)=2x2+1;③x2=4;④(2x)2=(x-1)2 ⑤$\frac{{x}^{2}-3x}{x}$=2x2.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
18.下列运算正确的是( )
| A. | (x-1)2=x2-2x-1 | B. | (a-b)2=a2-b2 | C. | (a+m)(b+n)=ab+mn | D. | (m+n)(-m+n)=-m2+n2 |
15. 如图,△ABC≌△DEF,则图中相等的线段有( )
如图,△ABC≌△DEF,则图中相等的线段有( )
 如图,△ABC≌△DEF,则图中相等的线段有( )
如图,△ABC≌△DEF,则图中相等的线段有( )| A. | 3组 | B. | 4组 | C. | 5组 | D. | 6组 |
 在某月的日历上用正方形圈到a、b、c、d四个数(如图),如果d=18,那么a+b+c=38.
在某月的日历上用正方形圈到a、b、c、d四个数(如图),如果d=18,那么a+b+c=38.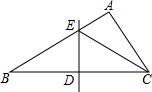 如图,在△ABC中,DE是BC的垂直平分线.
如图,在△ABC中,DE是BC的垂直平分线.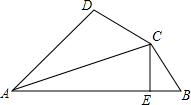 如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有( )个
如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有( )个