题目内容
14. 如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.(1)请你在所给的网格中画出四边形A1B1C1D1,使四边形A1B1C1D1和四边形ABCD关于直线l对称;
(2)在(1)的条件下,结合所画的图形,直接写出四边形A1B1C1D1的面积=$\frac{13}{2}$
(3)在直线l上画出点Q,使QA+QC最小.
分析 (1)根据轴对称的性质画出图形即可;
(2)利用矩形的面积减去四个顶点上三角形的面积即可;
(3)作出点A关于直线l的对称点A1,连接A1C,即可得到结论.
解答  解:(1)如图所示.
解:(1)如图所示.
(2)S四边形A1B1C1D1=3×4-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×2
=12-1-1-$\frac{3}{2}$-2
=$\frac{13}{2}$;
故答案为:$\frac{13}{2}$;
(3)连接CA1交直线l于Q,则点Q即为所求.
点评 本题考查的是轴对称-最短路线问题,作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
相关题目
19.函数y=$\sqrt{2-x}$+$\frac{1}{x-3}$中自变量x的取值范围是( )
| A. | x=3 | B. | x≤2 | C. | x<2且x≠3 | D. | x≤2且x≠3 |
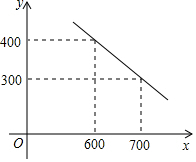 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.