题目内容
19.点P在正方形ABCD内,且△PAB是等边三角形,那么∠DCP为( )| A. | 15° | B. | 18° | C. | 22.5° | D. | 30° |
分析 先根据已知求得∠DAP=30°,再证明AB=AD=AP=BC,进而求出∠PCB的度数,再求出∠DCP的度数即可.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠CBA=90°,∵△PAB是等边三角形,
∴∠PAB=∠PBA=60°,PA=PB=AB,
∴∠DAP=∠CBP=30°,PB=BC,
∴∠PCB=$\frac{180°-30°}{2}$=75°,
∴∠DCP=90°-75°=15°.
故选A.
点评 本题考查了正方形和等边三角形的性质:正方形的四条边都相等,四个角都是直角;等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.

练习册系列答案
相关题目
9.已知抛物线y=ax2+2ax+m(a>0)经过点(-4,y1)、(-2,y2),(1,y3),则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y1>y3>y2 | D. | y3>y1>y2 |
14.以下列各组线段长为边能组成三角形的是( )
| A. | 1cm,2cm,4cm | B. | 2cm,4cm,6cm | C. | 4cm,6cm,8cm | D. | 5cm,6cm,12cm |
4.若三个有理数的和为0,则( )
| A. | 三个数可能同号 | |
| B. | 三个数一定为0 | |
| C. | 一定有两个数互为相反数 | |
| D. | 一定有一个数等于其余两个数的和的相反数 |
11.在电子显微镜下测得一个圆球体细胞的直径是5×104纳米,2×103个这样的细胞排成的细胞链的长是( )
| A. | 106纳米 | B. | 107纳米 | C. | 108纳米 | D. | 109纳米 |
8.正九边形的每个外角的度数是( )
| A. | 40° | B. | 90° | C. | 120° | D. | 360° |
9.下列命题正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直且相等的四边形是正方形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
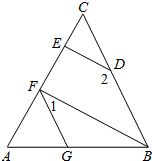 如图,∠AGF=∠ABC,∠1+∠2=180°,
如图,∠AGF=∠ABC,∠1+∠2=180°,