题目内容
如图1,P是∠AOB的平分线OC上的一点,过点分别作OA,OB的垂线,垂足分别为点D和点H,E是线段上一点是线段OD上一点,且DE=FH;
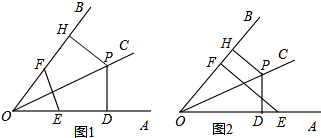
(1)证明:点P在线段EF的中垂线上;
(2)如果点E在射线DA上,如图2,其余的条件都不变,那么(1)的结论是否依然成立?

(1)证明:点P在线段EF的中垂线上;
(2)如果点E在射线DA上,如图2,其余的条件都不变,那么(1)的结论是否依然成立?
考点:角平分线的性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:(1)根据角平分线上的点到角的两边距离相等可得PD=PH,再利用“HL”证明Rt△OPH和Rt△OPD全等,根据全等三角形对应边相等可得OD=OH,然后求出OE=OF,再根据到线段两端点距离相等的点在线段的垂直平分线证明;
(2)连接PE、PF,根据角平分线上的点到角的两边距离相等可得PD=PH,再利用“边角边”证明△PED和△PFH全等,根据全等三角形对应边相等可得PE=PF,根据到线段两端点距离相等的点在线段的垂直平分线证明.
(2)连接PE、PF,根据角平分线上的点到角的两边距离相等可得PD=PH,再利用“边角边”证明△PED和△PFH全等,根据全等三角形对应边相等可得PE=PF,根据到线段两端点距离相等的点在线段的垂直平分线证明.
解答: (1)证明:∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,
(1)证明:∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,
∴PD=PH,
在Rt△OPH和Rt△OPD中,
,
∴Rt△OPH≌Rt△OPD(HL),
∴OD=OH,
∵DE=FH,
∴OD-DE=OH-FH,
即OE=OF,
∴点P在线段EF的中垂线上;
(2)解:结论依然成立.
理由如下:连接PE、PF,
∵PD⊥OA,PH⊥OB,
∴∠PDE=∠PHF=90°,
∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,
∴PD=PH,
在△PED和△PFH中,
,
∴△PED≌△PFH(SAS),
∴PE=PF,
∴点P在线段EF的中垂线上.
 (1)证明:∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,
(1)证明:∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,∴PD=PH,
在Rt△OPH和Rt△OPD中,
|
∴Rt△OPH≌Rt△OPD(HL),
∴OD=OH,
∵DE=FH,
∴OD-DE=OH-FH,
即OE=OF,

∴点P在线段EF的中垂线上;
(2)解:结论依然成立.
理由如下:连接PE、PF,
∵PD⊥OA,PH⊥OB,
∴∠PDE=∠PHF=90°,
∵OP是∠AOB的平分线,PD⊥OA,PH⊥OB,
∴PD=PH,
在△PED和△PFH中,
|
∴△PED≌△PFH(SAS),
∴PE=PF,
∴点P在线段EF的中垂线上.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,线段垂直平分线上的点到两端点的距离相等的性质,熟记各性质并求出三角形全等是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,在矩形ABCD中,AD=2AB=2,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,那么AM=
如图,在矩形ABCD中,AD=2AB=2,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,那么AM= 如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时,两针所指区域的数字和为偶数的概率是
如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时,两针所指区域的数字和为偶数的概率是