题目内容
在等腰梯形ABCD中,AB=CD=5,AD=4,BC=10,AB上有一点M,设BM=x,四边形AMCD的面积为y,则y与x的函数关系式为 .
考点:等腰梯形的性质
专题:
分析:作AG⊥BC于G,MH⊥BC于H,得出MH∥AG,根据平行线分线段成比例定理得出MB:AB=MH:AG,根据等腰梯形的性质和勾股定理求得高AG=4,然后根据MB:AB=MH:AG,求得MH的长,最后根据四边形AMCD的面积=S梯形ABCD-S△MBC即可得出结论.
解答: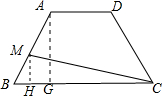 解:作AG⊥BC于G,MH⊥BC于H,
解:作AG⊥BC于G,MH⊥BC于H,
∴MH∥AG,
∴MB:AB=MH:AG,
∵在等腰梯形ABCD中,AD=4,BC=10,
∴BG=
(BC-AD)=
(10-4)=3,
∵在RT△ABG中,AB=5,
∴AG=
=
=4,
∵BM=x,
∴
=
,
∴MH=
x,
∴y=S梯形ABCD-S△MBC=
(AD+BC)•AG-
BC•MH=
(4+10)×4-
×10×
x=28-4x,
即y=-4x+28.
故答案为y=-4x+28.
 解:作AG⊥BC于G,MH⊥BC于H,
解:作AG⊥BC于G,MH⊥BC于H,∴MH∥AG,
∴MB:AB=MH:AG,
∵在等腰梯形ABCD中,AD=4,BC=10,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∵在RT△ABG中,AB=5,
∴AG=
| AB2-BG2 |
| 52-32 |
∵BM=x,
∴
| x |
| 5 |
| MH |
| 4 |
∴MH=
| 4 |
| 5 |
∴y=S梯形ABCD-S△MBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
即y=-4x+28.
故答案为y=-4x+28.
点评:本题考查了等腰梯形的性质,勾股定理的应用,四边形面积的求法等,作出辅助线构建直角三角形求得AG是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知抛物线y=-
如图,已知抛物线y=- 已知抛物线y=-x2+bx-c的部分图象如图.
已知抛物线y=-x2+bx-c的部分图象如图.
 某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要
某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要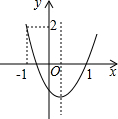 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②b2-4ac>0;③a+b+c=0; ④a+c=1
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②b2-4ac>0;③a+b+c=0; ④a+c=1