题目内容
1.在△ABC中,∠C=90°,若c=10,a:b=3:4,则S△ABC=24.分析 设a=3x,b=4x,利用勾股定理a2+b2=c2,可解出x的值,进而得出a及b的值,则易求S△ABC的值.
解答 解:设a=3x,b=4x,
则a2+b2=c2,即9x2+16x2=100,
解得:x=2,
所以a=3×2=6,b=4×2=8.
则S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$×6×8=24.
故答案为24.
点评 本题考查勾股定理的知识,属于基础题,掌握“在直角三角形中,两条直角边长的平方之和等于斜边长的平方”是解答本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
11. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF•DE=CE•CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:DF•DE=CE•CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
12.代数式-3x2y,0,6x+y,$\frac{x+y}{4}$,$\frac{b}{a}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
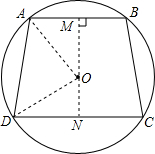 如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.
如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积. 如图,已知点A、B在直线l的同侧,在l上求作一点M,使得AM+BM最小.
如图,已知点A、B在直线l的同侧,在l上求作一点M,使得AM+BM最小.