题目内容
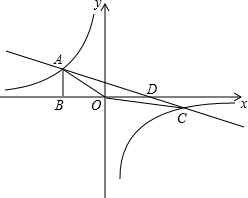 如图,反比例函数y1=
如图,反比例函数y1=| k |
| x |
(1)求k和n的值;
(2)若一次函数y2=ax+b的图象经过点A,且与反比例函数y1=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由△AOB的面积为3,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=-3代入,即可求出n的值;
(2)把把y=-1代入y=-
得,得出C的坐标为(6,-1),根据A、C的坐标利用待定系数法即可求出这个直线AC的解析式,根据S△AOC=S△AOD+S△DOC即可求得三角形AOC的面积.
(2)把把y=-1代入y=-
| 6 |
| x |
解答:解:(1)∵反比例函数y1=
的图象经过点A(-3,n)过点A作AB⊥x轴于B,△AOB的面积为3.
∴
OB×AB=3,
即
×3×n=3,
∴n=2,
∴A(-3,2),
∴k=xy=-6,
(2)把y=-1代入y=-
得,x=6,
∴C的坐标为(6,-1),
∵一次函数y2=ax+b的图象经过点A、C,
∴
,解得
,
∴直线AC的解析式为y=-
x+1,
令y=0,则0=-
x+1,解得x=3,
∴D的坐标为(3,0),
∴S△AOC=S△AOD+S△DOC=
OD•yA+
OD•yC=
×3×2+
×2×1=4.
| k |
| x |
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
∴n=2,
∴A(-3,2),
∴k=xy=-6,
(2)把y=-1代入y=-
| 6 |
| x |
∴C的坐标为(6,-1),
∵一次函数y2=ax+b的图象经过点A、C,
∴
|
|
∴直线AC的解析式为y=-
| 1 |
| 3 |
令y=0,则0=-
| 1 |
| 3 |
∴D的坐标为(3,0),
∴S△AOC=S△AOD+S△DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了待定系数法求一次函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |

练习册系列答案
相关题目
如果有理数a,b,c满足关系式a<b<0<c,那么式子
的值( )
| bc-ac |
| ab2c2 |
| A、必为正数 | B、必为负数 |
| C、可正可负 | D、可能为0 |
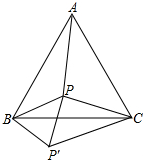 已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.
已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置. 如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论.
如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论.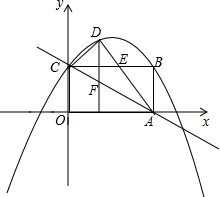 已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0,
已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0, 已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15,求△DEB的周长.
已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15,求△DEB的周长.