题目内容
若BD是等腰△ABC一腰上的高,且∠ABD=50°,则等腰△ABC的顶角的度数为 .
考点:等腰三角形的性质
专题:分类讨论
分析:根据直角三角形两锐角互余求出∠A,再分点A是顶角顶点,点A是底角或顶角顶点3种情况求解.
解答: 解:∵∠ABD=50°,BD是腰上的高,
解:∵∠ABD=50°,BD是腰上的高,
∴∠A=90°-∠ABD=90°-50°=40°,
①如图1,点A是顶角顶点时,顶角为∠A,是40°;
②如图2,点A是底角顶点时,
顶角∠BAC=180°-40°×2=100°,
③如图3,点A是顶角顶点时,
顶角∠BAC=180°-40°=140°,
综上所述,等腰△ABC的顶角的度数为40°或100°或140°.
故答案为:40°或100°或140°.
 解:∵∠ABD=50°,BD是腰上的高,
解:∵∠ABD=50°,BD是腰上的高,∴∠A=90°-∠ABD=90°-50°=40°,
①如图1,点A是顶角顶点时,顶角为∠A,是40°;
②如图2,点A是底角顶点时,
顶角∠BAC=180°-40°×2=100°,
③如图3,点A是顶角顶点时,
顶角∠BAC=180°-40°=140°,
综上所述,等腰△ABC的顶角的度数为40°或100°或140°.

故答案为:40°或100°或140°.
点评:本题考查了等腰三角形的性质,直角三角形两锐角互余,难点在于要分情况讨论.

练习册系列答案
相关题目
 如图,对称轴为直线l的抛物线y=ax2+bx+c与坐标轴交于点A、C,且OA=2OC=1.则下列结论:①当x<0时,y随x的增大而增大;②4a+2b+1>0;③b<
如图,对称轴为直线l的抛物线y=ax2+bx+c与坐标轴交于点A、C,且OA=2OC=1.则下列结论:①当x<0时,y随x的增大而增大;②4a+2b+1>0;③b<| 8 |
| 5 |
| A、0 | B、1 | C、2 | D、3 |
下列运算中正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y= 如图,如果从半径为9cm的圆形纸片剪去
如图,如果从半径为9cm的圆形纸片剪去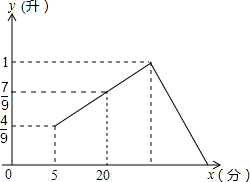 有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的
有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的