题目内容
10.如果方程(x-2)(x2-3x+m)=0的三根可作为一个三角形的三边长,则实数m的取值范围为$\frac{5}{4}$<m≤$\frac{9}{4}$.分析 利用两数相乘积为0得到两个方程,求出x的值,根据三角形三边关系列出不等式,求出解集即可确定出m的范围.
解答 解:方程(x-2)(x2-3x+m)=0,
得到x-2=0或x2-3x+m=0,
解得:x=2或x=$\frac{3±\sqrt{9-4m}}{2}$,
∵方程的三根可作为一个三角形的三边长,
∴$\frac{3-\sqrt{9-4m}}{2}$>0,且9-4m≥0,$\frac{3+\sqrt{9-4m}}{2}$-$\frac{3-\sqrt{9-4m}}{2}$=$\sqrt{9-4m}$<2,
解得:$\frac{5}{4}$<m≤$\frac{9}{4}$.
故答案为:$\frac{5}{4}$<m≤$\frac{9}{4}$
点评 此题考查了解一元二次方程-因式分解法,以及三角形三边关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.-(3x-1)(x+2y)是下列哪个多项式的分解结果( )
| A. | 3x2+6xy-x-2y | B. | 3x2-6xy+x-2y | C. | x+2y+3x2+6xy | D. | x+2y-3x2-6xy |
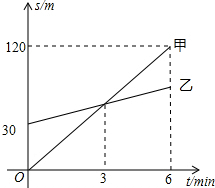 甲、乙两名运动员练习长跑,乙先跑30m,然后甲沿相同的路线与乙一同跑步,设甲跑的路程为s1(m),乙跑的路程为s2(m),甲与乙一同跑步所用的时间(从甲开始跑步计时)为t(min),s1、s2与t之间的部分函数图象如图所示.
甲、乙两名运动员练习长跑,乙先跑30m,然后甲沿相同的路线与乙一同跑步,设甲跑的路程为s1(m),乙跑的路程为s2(m),甲与乙一同跑步所用的时间(从甲开始跑步计时)为t(min),s1、s2与t之间的部分函数图象如图所示.


