题目内容
4.矩形ABCD的周长为20cm,对角线AC、BD相交于点O,若△AOB与△BOC的周长差为4cm,则矩形ABCD中较长的边长是7cm.分析 由矩形的性质得出OA=OB=OC=OD,再由已知条件得出AB+BC=10cm,AB-BC=4cm,求出AB即可.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,AB=CD,AD=BC,
∴OA=OB=OC=OD,
∵矩形ABCD的周长为20cm,
∴AB+BC=10cm①,
∵△AOB与△BOC的周长差为4cm,
∴AB+OA+OB-(BC+OB+OC)=4cm,
∴AB-BC=4cm②,
由①+②得:2AB=14cm,
∴AB=7cm,
即矩形ABCD中较长的边长是7cm;
故答案为:7cm.
点评 本题考查了矩形的性质、三角形与矩形周长的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
12. 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )| A. | -1<x<3 | B. | -1<x≤3 | C. | -1≤x<3 | D. | -1≤x≤3 |
19.下列各式正确的是( )
| A. | 2a2-a2=2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | ($\sqrt{5}$)2=25 | D. | $\sqrt{(-1)^{2}}$=1 |
16.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 等边三角形 | C. | 平行四边形 | D. | 矩形 |
13.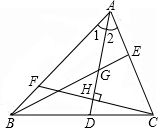 如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
 如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )| A. | AD是△ABE的角平分线 | B. | BE是△ABD边AD上的中线 | ||
| C. | CH为△ACD边AD上的高 | D. | AH为△ABC的角平分线 |
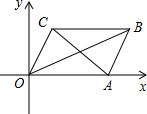 如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.
如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.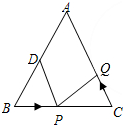 如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为2或3.2厘米/秒.
如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为2或3.2厘米/秒.