题目内容
14.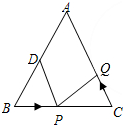 如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为2或3.2厘米/秒.
如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为2或3.2厘米/秒.
分析 根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可.
解答 解:∵AB=16cm,BC=10cm,点D为AB的中点,
∴BD=$\frac{1}{2}$×16=8cm,
设点P、Q的运动时间为t,则BP=2t,
PC=(10-2t)cm
①当BD=PC时,10-2t=8,
解得:t=1,
则BP=CQ=2,
故点Q的运动速度为:2÷1=2(厘米/秒);
②当BP=PC时,∵BC=10cm,
∴BP=PC=5cm,
∴t=5÷2=2.5(秒).
故点Q的运动速度为8÷2.5=3.2(厘米/秒).
故答案为:2或3.2厘米/秒
点评 本题考查了全等三角形的对应边相等的性质,等边对等角的性质,根据对应角分情况讨论是本题的难点.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
19.二元一次方程x-2y=4( )
| A. | 有一个解且只有一个解 | B. | 无解 | ||
| C. | 有无数多个解 | D. | 有两个解且只有两个解 |
4.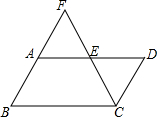 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )| A. | △AEF≌△CED | B. | CF=AD | C. | AF=CD | D. | BF=CF |
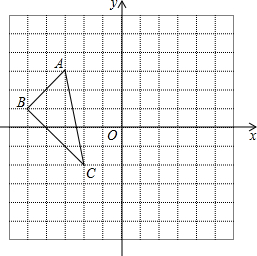 按要求画出图形:
按要求画出图形: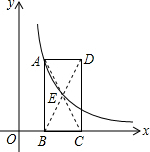 已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).