题目内容
15.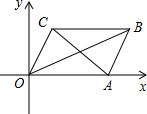 如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.
如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.(1)直接写出点P的坐标是(3,$\sqrt{3}$);
(2)若一次函数y=x+b的图象经过点P,求b的值;
(3)若一次函数y=x+m的图象与四边形OABC有两个公共点时,直接写出m的取值范围.
分析 (1)证明CA是∠BCO的平分线,又根据OB是∠AOC的平分线,即可证明P是AC的中点,首先求得C的坐标,则P的坐标即可求解;
(2)把P的坐标代入解析式即可求得b的值;
(3)首先求得一次函数y=x+m经过A和C时m的值,则m的取值范围即可求解.
解答 解:(1)∵OB平分∠AOC,OA=OC,
∴AC⊥OB,
∵OA∥BC,
∴∠OBC=∠AOB,
又∵∠AOB=∠BOC,
∴∠BOC=∠OBC,
∴CO=CB,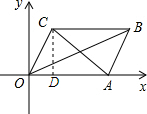
又∵AC⊥OB,
∴CA平分∠BCO,
又∵点P到四边形OABC四条边的距离相等.
∴P就是AC和OB的交点.
作CD⊥OA于点D.
在直角△OCD中,CD=OCsin∠AOC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,CD=CO•cos60°=4×$\frac{1}{2}$=2,
则C的坐标是(2,2$\sqrt{3}$).
∴P的坐标是($\frac{2+4}{2}$,$\frac{2\sqrt{3}+0}{2}$),即(3,$\sqrt{3}$).
故答案是:(3,$\sqrt{3}$);
(2)把(3,$\sqrt{3}$)代入y=x+b得3+b=$\sqrt{3}$,解得b=$\sqrt{3}$-3;
(3)当y=x+m经过点A时,把(4,0)代入得4+m=0,解得m=-4,
当y=x+m经过点C(3,$\sqrt{3}$)时,则3+m=$\sqrt{3}$,解得m=$\sqrt{3}$-3.
则当$\sqrt{3}$-3<m<-4.
点评 本题考查了待定系数法求函数解析式与角平分线的性质,利用三角函数求得C的坐标,正确证明P是AC的中点是关键.

练习册系列答案
相关题目
18.已知a>0,则下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{a}$=$\sqrt{2a}$ | B. | $\sqrt{{a}^{2}}$-$\sqrt{a}$=$\sqrt{a}$ | C. | $\sqrt{a}×\sqrt{a}$=a2 | D. | $\sqrt{a}$$÷\sqrt{a}$=1 |
7.已知菱形的边长和一条对角线长均为2cm,则菱形的面积为( )cm2.
| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 已知,如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.
已知,如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.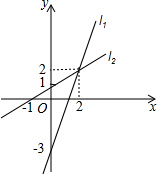 已知l1、l2的解析式分别为y1=ax+b,y2=mx+n(a>m>0),如图是l1、l2的图象,根据图象回答以下问题:
已知l1、l2的解析式分别为y1=ax+b,y2=mx+n(a>m>0),如图是l1、l2的图象,根据图象回答以下问题: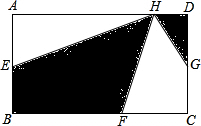 如图所示,长方形ABCD中,AE=EB,BC=3BF,CG=GD,H是AD上任意一点,则图中阴影部分的面积是长方形ABCD的几分之几?
如图所示,长方形ABCD中,AE=EB,BC=3BF,CG=GD,H是AD上任意一点,则图中阴影部分的面积是长方形ABCD的几分之几?