三角形两边长分别为3和6.第三边的长是方程x2-15x+50=0的两根.则该三角形的周长为( )A．14B．15C．19D．14或19 题目和参考答案——青夏教育精英家教网—

题目内容

2．三角形两边长分别为3和6，第三边的长是方程x²-15x+50=0的两根，则该三角形的周长为（　　）

A．

B．

C．

D．

14或19

分析先求出方程x²-15x+50=0的两根，再根据三角形的三边关系定理，得到合题意的边，进而求得三角形周长即可．

解答解：解方程x²-15x+50=0得，
x=5或10，
即第三边长为5或10．
边长为10，3，6不能构成三角形；
而5，3，6能构成三角形，
所以三角形的周长为3+5+6=14．
故选：A．

点评此题主要考查了因式分解法解一元二次方程以及三角形的三边关系，求三角形的周长，不能盲目地将三边长相加起来，需要检验三边长能否成三角形．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

12．已知$\sqrt{x+1}$+（y-2015）²=0，则x^y=-1．

13．在（-1）²⁰¹⁵，|-1|³，-（-1）¹⁸，1⁸这四个有理数中，负数共有（　　）

10．求下列各式中x的值．
（1）4x²-49=0
（2）（x+1）³=-8．

17．

如图，矩形ABCD中，BC=2，DC=4，以AB为直径的半圆O与DC相切于点E，则阴影部分的面积为多少？（结果保留π）

7．

如图，B是线段AD上一动点，沿A→D→A以2cm/s的速度往返运动1次，C是线段BD的中点，AD=10cm，设点B运动时间为t秒（0≤t≤10）．
（1）当t=2时，①AB=4cm．②求线段CD的长度．
（2）①点B沿点A→D运动时，AB=2tcm；
②点B沿点D→A运动时，AB=20-2tcm．（用含t的代数式表示AB的长）
（3）在运动过程中，若AB中点为E，则EC的长是否变化，若不变，求出EC的长；若发生变化，请说明理由．

14．

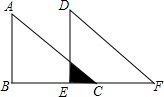如图，等腰直角三角形ABC中，∠ABC=90°，AB=BC=4cm，将△ABC沿BC方向平移3cm后，得△DEF，则图中阴影部分的面积为$\frac{1}{2}$cm²．

11．抛物线y=ax²+bx+c与x轴的交点是（-3，0），（1，0），则这条抛物线的对称轴是（　　）

12．

如图，等边三角形ABC中，BD是AC边上的中线，BD=BE，则∠EDA=15 度．

试题分类