题目内容
16. 如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O于点A,如果PA=4,PB=2,那么线段BC的长等于( )
如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O于点A,如果PA=4,PB=2,那么线段BC的长等于( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 如图,连接OA.根据切线的性质得到∠OAP=90°,所以在直角△AOP中,利用勾股定理来求该圆的半径,则易求直径BC的长度.
解答 解:设该圆的半径为r(r>0),
如图,连接OA,
∵PA切⊙O于点A,
∴OA⊥AP,即∠OAP=90°,
又∵PA=4,PB=2,
∴在直角△AOP中,利用勾股定理得到:PA2+OA2=OP2,即42+r2=(r+2)2,
则r=3,
∴⊙O的直径BC=2r=6,
故选D.
点评 本题考查了切线的性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题是解答此题的关键.

练习册系列答案
相关题目
7.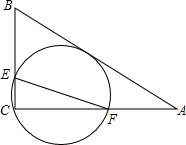 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )| A. | 随圆的大小变化而变化,但没有最值 | |
| B. | 最大值为4.8 | |
| C. | 有最小值 | |
| D. | 为定值 |
1.已知|a|=3,|b|=4,且ab<0,则a-b的值为( )
| A. | 1或7个 | B. | 1-或7 | C. | ±1个 | D. | ±7 |
 如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5.
如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=4.
如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=4.