题目内容
20.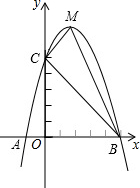 已知,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,其中A点坐标(-1,0),点C坐标为(0,5),另外抛物线过点(1,8),M为它的顶点,
已知,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,其中A点坐标(-1,0),点C坐标为(0,5),另外抛物线过点(1,8),M为它的顶点,(1)求抛物线的解析式;
(2)求△AMB的面积S△AMB.
分析 (1)将已知的三点坐标代入抛物线中,即可求得抛物线的解析式;
(2)令y=-x2+4x+5=0,求出点B的坐标,即可求出AB的长,再求出二次函数的顶点坐标,根据三角形面积计算公式求出答案.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的图象经过(-1,0)、(0,5)和(1,8),
∴$\left\{\begin{array}{l}{a-b+c=0}\\{c=5}\\{a+b+c=8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=5}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x+5;
(2)令y=-x2+4x+5=0,
解得x1=-1,x2=5,
∴B点坐标为(5,0),
∴AB=5-(-1)=6,
∵y=-x2+4x+5,
∴y=-(x-2)2+9,
∴抛物线图象的顶点坐标为(2,9),
∴S△AMB=$\frac{1}{2}$×6×9=27.
点评 本题考查了抛物线与x轴交点以及待定系数法求二次函数解析式的知识,解答本题的关键是求出点B的坐标,此题难度不大.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
5.已知等腰三角形的一个角的度数是50°,那么它的其它两个角的度数是( )
| A. | 50°,80° | B. | 65°,65° | ||
| C. | 50°,80°或65°,65° | D. | 60°,70°或30°,100° |
12.下列图形一定相似的是( )
| A. | 两个矩形 | B. | 两个菱形 | ||
| C. | 两个等腰直角三角形 | D. | 两个直角三角形 |
 如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.
如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.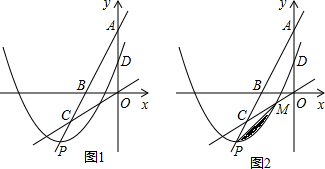
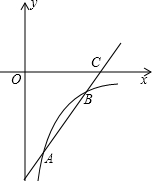 如图,已知一次函数y1=kx+b的图象交反比例函数y2=$-\frac{4-2m}{x}$(x>0)图象于点A、B,交x轴于点C.
如图,已知一次函数y1=kx+b的图象交反比例函数y2=$-\frac{4-2m}{x}$(x>0)图象于点A、B,交x轴于点C.
 已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).画出以点O为位似中心,放大△ABC到原来的2倍的△A′B′C′.
已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).画出以点O为位似中心,放大△ABC到原来的2倍的△A′B′C′.