题目内容
15．已知$x+\frac{1}{x}=3$，那么${x^2}+\frac{1}{x^2}$=7，${x^4}+\frac{1}{x^4}$=47．分析 根据完全平方公式得出x2+$\frac{1}{{x}^{2}}$=（x+$\frac{1}{x}$）2-2•x•$\frac{1}{x}$，代入求出即可；
根据完全平方公式得出x4+$\frac{1}{{x}^{4}}$=（x2+$\frac{1}{{x}^{2}}$）2-2•x2•$\frac{1}{{x}^{2}}$，代入求出即可．
解答 解：∵x+$\frac{1}{x}$=3，
∴x2+$\frac{1}{{x}^{2}}$=（x+$\frac{1}{x}$）2-2•x•$\frac{1}{x}$=32-2=7，
∴x4+$\frac{1}{{x}^{4}}$=（x2+$\frac{1}{{x}^{2}}$）2-2•x2•$\frac{1}{{x}^{2}}$=49-2=47，
故答案为：7，47．
点评 本题考查了完全平方公式的应用，能正确运用公式展开是解此题的关键，注意：完全平方公式为：（a+b）2=a2+2ab+b2和（a-b）2=a2-2ab+b2，此题是基础题目，难度不大．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
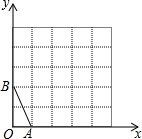在方格纸中，每个小格的顶点称为格点，以格点的连线为边的三角形称为格点三角形，如图所示的5×5的方格纸中，如果想作格点△ABC与△OAB相似（相似比不能为1），则C点坐标为（4，4）或（5，2）．
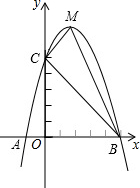已知，如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C，其中A点坐标（-1，0），点C坐标为（0，5），另外抛物线过点（1，8），M为它的顶点，