题目内容
13.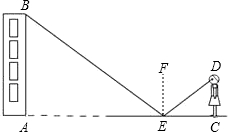 小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
分析 根据反射角等于入射角可得∠AEB=∠CED,则可判断Rt△AEB∽Rt△CED,根据相似三角形的性质得$\frac{AB}{1.6}$=$\frac{21}{2.5}$,然后利用比例性质求出AB即可.
解答 解:根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴$\frac{AB}{CD}$=$\frac{AE}{CE}$,即$\frac{AB}{1.6}$=$\frac{21}{2.5}$,
解得:AB=13.44.
答:教学楼的高度为13.44m.
点评 本题考查了相似三角形的应用:利用入射与反射构造相似三角形,然后利用相似三角形的性质即相似三角形的对应边的比相等解决问题.

练习册系列答案
相关题目
18. 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
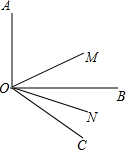 如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.
如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.
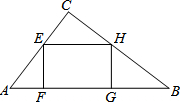 如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.
如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.